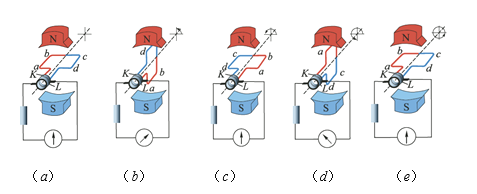
题目内容
【题目】如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右侧,杆上套有一质量m=2kg的小球A。半径R=0.3m的光滑半圆形细轨道竖直的固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B。用一条不可伸长的柔软细绳,通过定滑轮将两个小球连接起来,杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响。现给小球A一个水平向右的恒力F=50N,(g=10m/s2),则( )
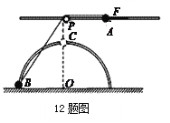
A. 当小球B运动到C处时小球A的动能为20J
B. 小球B运动到C处时的速度大小为![]() m/s
m/s
C. 小球B被拉到与小球A速度大小相等时,sin∠OPB=![]()
D. 小球B从地面运动到C处的过程中,小球B的动能增加了6J
【答案】BC
【解析】
由几何知识可知,小球B从B运动到C过程中,球A的位移为![]() ,小球B运动到C处时,已无沿绳的分速度,所以球A的速度为零,即A的动能等于零,设小球B的速度为v,根据功能关系可得
,小球B运动到C处时,已无沿绳的分速度,所以球A的速度为零,即A的动能等于零,设小球B的速度为v,根据功能关系可得![]() ,解得
,解得![]() ,故A错误;B正确;由题意可知,当小球B只具有沿绳的速度时,与小球A的速度大小相等,当绳与圆形轨道相切时,小球B只具有沿绳的速度,与小球A的大小相等,此时BO垂直于BP,由几何知识可知,
,故A错误;B正确;由题意可知,当小球B只具有沿绳的速度时,与小球A的速度大小相等,当绳与圆形轨道相切时,小球B只具有沿绳的速度,与小球A的大小相等,此时BO垂直于BP,由几何知识可知,![]() ,故C正确;小球B从地面运动到C处的过程中,小球B的动能增加了
,故C正确;小球B从地面运动到C处的过程中,小球B的动能增加了![]() ,故D错误;故选BC
,故D错误;故选BC

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目