Question

【题目】如图所示，真空中存在空间范围足够大的、水平向右的匀强电场．在电场中，若将一个质量为m、带正电的小球由静止释放，运动中小球的速度与竖直方向夹角为37°（取sin37°=0．6，cos37°=0．8）。现将该小球从电场中某点以初速度v0。竖直向上抛出。求运动过程中：

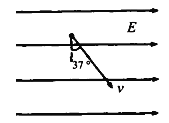
（1）小球受到的电场力的大小及方向；

（2）小球从抛出点至最高点的电势能变化量；

（3）小球的最小速度的大小及方向。

Answer 1

【答案】（1）电场力为，方向水平向右（2）

（3），与电场方向夹角为37°斜向上

【解析】试题分析：（1）小球所受电场力与重力的合力一定沿速度v方向，即有： ，得，方向水平向右；

（2）竖直方向小球做竖直上抛运动，故上升时间为；上升的高度为

到最高点时速度为水平方向，设为，则有： ，

o由动能定理得得，

即电势能减小了。

将初速度分解为沿v反方向的分量和垂直此方向的分速度；小球在方向做类竖直上抛运动，到“最高点”处速度仅有垂直于方向的分速度，此时合力对小球做的负功最多，即小球的速度最小，且为，方向与v垂直，斜向右上方，即与电场E方向夹角为37°，斜向上。