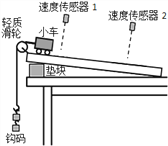
��Ŀ����
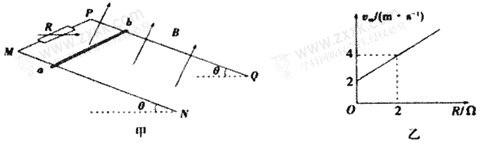
����Ŀ����ͼ����ʾ��MN��PQ����ƽ�еĹ⻬���������ˮƽ���300�ǹ̶���M��P֮��ӵ�����R���������ڿռ������ǿ�ų����ų�����ֱ�ڹ��ƽ�����ϣ��Ÿ�Ӧǿ��Ϊ2.5T������Ϊm�Ľ�����abˮƽ�����ڹ���ϣ���������ֱ��������ab�����·�ĵ���ֵΪr���ִӾ�ֹ�ͷŸ�ab���������ٶ�Ϊvm���ı���������ֵR���õ�vm��R�Ĺ�ϵ��ͼ����ʾ����֪������Ϊ![]() ���������ٶ�gȡ
���������ٶ�gȡ![]() ������㹻���ҵ��費�ơ�
������㹻���ҵ��費�ơ�
��1����![]() ʱ�����ab�����»�ʱ������Ӧ�綯��E�Ĵ�С�����жϸ��еĵ�������
ʱ�����ab�����»�ʱ������Ӧ�綯��E�Ĵ�С�����жϸ��еĵ�������
��2���������˵�����m����ֵr��
��3����![]() ʱ���Ӿ�ֹ�ͷ�ab�ˣ���ab�˼����˶��Ĺ����У���·˲ʱ�綯��ÿ����1Wʱ���������Ը��������٣�
ʱ���Ӿ�ֹ�ͷ�ab�ˣ���ab�˼����˶��Ĺ����У���·˲ʱ�綯��ÿ����1Wʱ���������Ը��������٣�
���𰸡���1��10V b��a ��2��5kg 2�� ��3��0.6 J
�����������������ab�������»�ʱ�ٶ����R=0ʱ������ͼ��������ٶȣ���E=BLv�����Ӧ�綯�ƣ������ֶ����жϸ�Ӧ�����ķ�����E=BLv���պϵ�·ŷķ���ɺͼ�ƽ���������Ƶ����˵�����ٶ�v��R�ı���ʽ�����ͼ������壬���˵�����m����ֵr����R=4��ʱ����������ٶȣ����ݹ��ʹ�ʽ�õ���·��˲ʱ�繦�ʵı仯�����ٸ��ݶ��ܶ������������Ը����Ĺ�W��
��1����ͼ��֪��r=0ʱ����������v=2m/s���ٶ��˶���
�綯��Ϊ��E=BLv=2.5��2��2V=10V
�����ֶ����жϵ�֪�����е��������b��a
��2��������ٶ�Ϊvm�����и�Ÿ��߲����ĸ�Ӧ�綯�� E=BL vm
�ɱպϵ�·��ŷķ���ɣ� ![]()
�˴ﵽ����ٶ�ʱ������ mgsin����BIL=0
��E=BL vm �ɵ��� ![]()
��![]() ��
�� ![]() �������ݴ�����ʽ
�������ݴ�����ʽ
��ã�m=5kg��r=2��
��3���������֪��E=BLv�� ����Ϊ�� ![]()
����ɵã� ![]()
���� ![]()
�ɶ��ܶ������� ![]()
�����ã� ![]()
�������ݽ����W=0.6 J

 �ƸԹھ��ο���ϵ�д�
�ƸԹھ��ο���ϵ�д�