题目内容
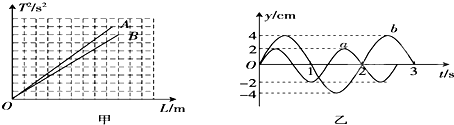
6．
如图，直线为光电子最大初动能与光子频率的关系，己知直线的纵、横截距分别为-a、b，电子电量为e，下列表达式正确的是（ ）| A． | 金属极限频率v0=b | |
| B． | 普朗克常量h=$\frac{b}{a}$ | |
| C． | 金属逸出功W0=a | |
| D． | 若入射光频率为2b，则光电子的初动能一定为a |
分析 根据光电效应方程EKm=hγ-W0=hγ-hγ0得出最大初动能与入射光频率的关系，通过图线的斜率和截距去求解．
解答 解：ABC、根据光电效应方程EKm=hγ-W0=hγ-hγ0知电子的最大初动能Ekm与入射光频率v不成正比，
图线的斜率表示普朗克常量，根据图线斜率可得出普朗克常量即h=$\frac{a}{b}$，所以逸出功为hb=a．
横轴截距表示最大初动能为零时的入射光频率，此时的频率等于金属的极限频率，也可能知道极限波长，故AC正确，B错误；
D、据光电效应方程可知，入射光频率为2b，初动能为：h•2b-a=a，所以光电子的最大初动能为a，并非光电子的初动能一定为a，故D错误．
故选：AC．
点评 解决本题的关键掌握光电效应方程EKm=hγ-W0=hγ-hγ0，知道逸出功与极限频率的关系和光电效应的特点
练习册系列答案
相关题目
16．
如图所示，水平传送带两端点A、B间的距离为L，传送带被锁定，处于静止状态．现用水平恒力F拉物体，使小物体以v1的速度由A点匀速滑行到B点．这一过程，拉力F做的功为W1、功率为P1，物体和传送带间因摩擦而产生的热量为Q1．随后让传送带以v2（v2＜v1）的速度匀速向左运动，仍用相同的力F使物体以v1的速度由A点匀速滑行到B点．这一过程，拉力F做的功为W2、功率为P2，物体和传送带间因摩擦而产生的热量为Q2，则下列关系中正确的是（ ）
如图所示，水平传送带两端点A、B间的距离为L，传送带被锁定，处于静止状态．现用水平恒力F拉物体，使小物体以v1的速度由A点匀速滑行到B点．这一过程，拉力F做的功为W1、功率为P1，物体和传送带间因摩擦而产生的热量为Q1．随后让传送带以v2（v2＜v1）的速度匀速向左运动，仍用相同的力F使物体以v1的速度由A点匀速滑行到B点．这一过程，拉力F做的功为W2、功率为P2，物体和传送带间因摩擦而产生的热量为Q2，则下列关系中正确的是（ ）| A． | W1=W2，P1＜P2，Q1=Q2 | B． | W1=W2，P1=P2，Q1＞Q2 | ||
| C． | W1＞W2，P1=P2，Q1＞Q2 | D． | W1＞W2，P1＞P2，Q1=Q2 |
14．
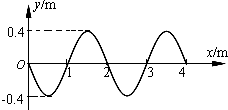一列简谐横波，沿x轴正方向传播，传播速度为10m/s，在t=0时的波形图如图所示，则下列说法正确的是（ ）
一列简谐横波，沿x轴正方向传播，传播速度为10m/s，在t=0时的波形图如图所示，则下列说法正确的是（ ）| A． | 此时x=1.25m处的质点正在做加速度减小的加速运动 | |
| B． | x=1m处的质点在做简谐运动，其振动方程为y=0.4sin（10πt）（m） | |
| C． | x=0.3m处的质点再经过0.08s可运动至波峰位置 | |
| D． | 若该波在传播过程中遇到一个尺寸为30 m的障碍物不能发生明显衍射现象 |
1．
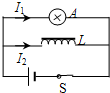如图所示的电路中，电键S闭合且电路达到稳定时，流过灯泡A和线圈L（RL≠0）的电流分别为I1和I2．在电键S切断的瞬间，为使小灯泡能比原来更亮一些，然后逐渐熄灭，则（ ）
如图所示的电路中，电键S闭合且电路达到稳定时，流过灯泡A和线圈L（RL≠0）的电流分别为I1和I2．在电键S切断的瞬间，为使小灯泡能比原来更亮一些，然后逐渐熄灭，则（ ）| A． | 必须使I2＞I1 | |
| B． | 与I1、I2大小无关，但必须使线圈自感系数L足够大 | |
| C． | 自感系数L越大，切断时间越短，则I2也越大 | |
| D． | 不论自感系数L多大，电键S切断瞬间I2只能减小，不会增大 |
11．
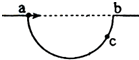如图所示，ab为半圆弧的水平直径，ab=1.5m，从a点平抛出一小球，小球下落0.3s后落到半圆弧的c点上，重力加速度g取10m/s2，则小球抛出的初速度v0为（ ）
如图所示，ab为半圆弧的水平直径，ab=1.5m，从a点平抛出一小球，小球下落0.3s后落到半圆弧的c点上，重力加速度g取10m/s2，则小球抛出的初速度v0为（ ）| A． | 1.5 m/s | B． | 0.5 m/s | C． | 3 m/s | D． | 4.5 m/s |
18．
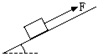如图所示，物体在平行于斜面向上、大小为5N的力F作用下，沿固定的粗糙斜面向上做匀速直线运动，物体与斜面间的滑动摩擦力（ ）
如图所示，物体在平行于斜面向上、大小为5N的力F作用下，沿固定的粗糙斜面向上做匀速直线运动，物体与斜面间的滑动摩擦力（ ）| A． | 等于零 | B． | 小于5N | C． | 等于5N | D． | 大于5N |
15．
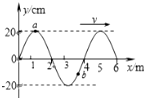如图所示，为某一沿x轴正向传播的一列简谐波在某一时刻的波形图，若其波速为200m/s，则下列说法中正确的是（ ）
如图所示，为某一沿x轴正向传播的一列简谐波在某一时刻的波形图，若其波速为200m/s，则下列说法中正确的是（ ）| A． | 从图示时刻开始，经0.01s后，质点a通过的路程为0.8m | |
| B． | 从图示时刻后的一小段时间里质点b的加速度将减小 | |
| C． | 若此波遇到另一列波并发生稳定的干涉现象，则另一列波的频率为50Hz | |
| D． | 若该波传播中遇到宽约4m的障碍物，能发生明显的衍射现象 |
2．
“卡西尼”号土星探测器在离土星表面高h的圆形轨道上飞行，环绕n周飞行时间为t，土星半径为R，已知引力常量为G，则下列关于土星质量M和平均密度ρ的表达式正确的是（ ）
“卡西尼”号土星探测器在离土星表面高h的圆形轨道上飞行，环绕n周飞行时间为t，土星半径为R，已知引力常量为G，则下列关于土星质量M和平均密度ρ的表达式正确的是（ ）| A． | M=$\frac{4{π}^{2}（R+h）}{G{t}^{2}}$；ρ=$\frac{3π（R+h）^{3}}{G{t}^{2}{R}^{3}}$ | |
| B． | M=$\frac{4{π}^{2}{n}^{2}（R+h）^{3}}{G{t}^{2}}$；ρ=$\frac{3π{n}^{2}（R+h）^{3}}{G{t}^{2}{R}^{3}}$ | |
| C． | M=$\frac{4{π}^{2}{t}^{2}（R+h）^{3}}{G{n}^{2}}$；ρ=$\frac{3π{t}^{2}（R+h）^{3}}{G{n}^{2}{R}^{3}}$ | |
| D． | M=$\frac{4{π}^{2}{n}^{2}（R+h）^{3}}{G{t}^{2}}$；ρ=$\frac{3π（R+h）^{2}}{G{t}^{2}{R}^{3}}$ |