题目内容
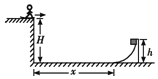
【题目】如图所示是一次娱乐节目中的一个游戏示意图，游戏装置中有一个光滑圆弧形轨道，高为h，固定在水平地面上，它的左端切线沿水平方向，左端与竖直墙面间的距离为x。竖直墙高为H，滑板运动员可从墙面的顶部沿水平方向飞到地面上。游戏规则是让一滑块从弧形轨道的最高点由静止滑下，当它滑到轨道底端时，滑板运动员立即以某一初速度水平飞出，当滑块在水平面上停止运动时，运动员恰好落地，并将滑块捡起就算获胜。已知重力加速度为g。（不计滑板的长度，运动员看做质点）求：
（1）滑块在圆弧形轨道底端的速度；
（2）滑块与地面间的动摩擦因数；
（3）滑板运动员要想获胜，他飞出时的初速度多大？
【答案】（1）
；（2）
；（3）
【解析】
（1）滑块下滑到斜面底端过程中，据动能定理
解得：
；
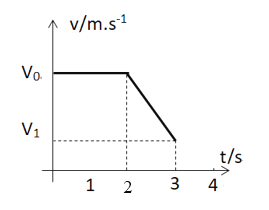
（2）滑块减速到零的时间与人做平抛运动的时间相同，据H＝
gt2
解得：
，
物块在地面上滑行时，据牛顿第二定律μmg＝ma，
据运动学公式
，
联立解得：
；
（3）当滑块在水平面上停止运动时，运动员恰好落地，故
，
解得：
；
练习册系列答案
相关题目
