题目内容
1．
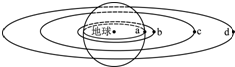四颗地球卫星a、b、c、d的排列位置如图所示，其中a是静止在地球赤道上还未发射的卫星，b是近地轨道卫星，c是地球同步卫星，d是高空探测卫星，关于四颗卫星下列说法正确的是（ ）| A． | c相对于b静止 | B． | 相同时间内b转过的弧长最长 | ||
| C． | a的向心加速度最大 | D． | d的运行周期可能是23 h |
分析 同步卫星的周期必须与地球自转周期相同，角速度相同，根据a=ω2r比较a与c的向心加速度大小，再比较c的向心加速度与g的大小．根据万有引力提供向心力，列出等式得出角速度与半径的关系，分析弧长关系．根据开普勒第三定律判断d与c的周期关系．
解答 解：A、b是近地轨道卫星，c是地球同步卫星，c相对于地面静止，近地轨道卫星相对于地面运动，所以c相对于b运动，A错误；
B、由$\frac{GMm}{{r}^{2}}$=mω2r得ω=$\sqrt{\frac{GM}{{r}^{3}}}$，卫星的半径越大，角速度越小，所以b的角速度最大，在相同时间内转过的弧长最长．故B正确；
C、同步卫星的周期必须与地球自转周期相同，角速度相同，则知a与c的角速度相同，根据a=ω2r知，c的向心加速度比a的向心加速度大．故C错误；
D、由开普勒第三定律$\frac{{r}^{3}}{{T}^{2}}$=k知，卫星的半径越大，周期越大，所以d的运动周期大于c的周期24h．故D错误；
故选：B．
点评 对于卫星问题，要建立物理模型，根据万有引力提供向心力，分析各量之间的关系，并且要知道同步卫星的条件和特点．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
如图所示．MN是足够长的光滑绝缘水平轨道．质量为m的带正电A球，以水平速度υ0射向静止在轨道上带正电的B球，至A、B相距最近时，A球的速度变为$\frac{υ_0}{4}$，已知A、B两球始终没有接触．求：
12．
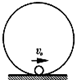如图所示，半径r=0.5m的光滑圆轨道被竖直固定在水平地面上，圆轨道最低处有一小球（小球的半径比r小很多）．现给小球一个水平向右的初速度v0，要使小球不脱离轨道运动，重力加速度g取10m/s2，则下列初速度v0范围能满足的是（ ）
如图所示，半径r=0.5m的光滑圆轨道被竖直固定在水平地面上，圆轨道最低处有一小球（小球的半径比r小很多）．现给小球一个水平向右的初速度v0，要使小球不脱离轨道运动，重力加速度g取10m/s2，则下列初速度v0范围能满足的是（ ）| A． | v0≥5m/s | B． | v0≥2$\sqrt{5}$m/s | C． | v0≥$\sqrt{5}$m/s | D． | v0≤$\sqrt{10}$m/s |
9．M、N两颗质量相同的卫星绕地球做匀速圆周运动，其轨道如图所示，则（ ）
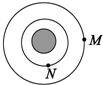
| A． | M与地球中心连线在相等的时间内转过的角度较大 | |
| B． | M的机械能大于N的机械能 | |
| C． | M、N的速度均大于第一宇宙速度 | |
| D． | M在相同的时间内经过的路程较短 |
6．下列说法正确的是（ ）
| A． | 简谐运动的周期与振幅无关 | |
| B． | 在弹簧振子做简谐运动的回复力表达式F=-kx中，F为振动物体受到的合外力，k为弹簧的劲度系数 | |
| C． | 在波传播方向上，某个质点的振动速度就是波的传播速度 | |
| D． | 在双缝干涉实验中，同种条件下用紫光做实验比红光做实验得到的条纹更宽 |
13．以下说法中正确的是（ ）
| A． | 单晶体的所有物理性质都具有各向异性 | |
| B． | 悬浮在液体中的花粉颗粒的无规则运动是热运动 | |
| C． | 相同温度下，氢分子的平均动能一定等于于氧分子的平均动能 | |
| D． | 随着分子间距离增大，分子间作用力减小，分子势能也减小 |
10．2014年11月21日，我国在酒泉卫星发射中心用快舟小型运载火箭成功将“快舟二号”卫星发射升空，并顺利进入预定轨道．我国已成为完整发射卫星-火箭一体化快速应急空间飞行器试验的国家，具有重要的战略意义．若快舟卫星的运行轨道均可视为圆轨道，“快舟一号”运行周期为T1、动能为Ek1；“快舟二号”运行周期为T2、动能为Ek2．已知两卫星质量相等．则两卫星的周期之比$\frac{T_1}{T_2}$为（ ）
| A． | $\frac{{{E_{k1}}}}{{{E_{k2}}}}$ | B． | $\frac{{{E_{k2}}}}{{{E_{k1}}}}$ | C． | $\sqrt{{{（{\frac{{{E_{k1}}}}{{{E_{k2}}}}}）}^3}}$ | D． | $\sqrt{{{（{\frac{{{E_{k2}}}}{{{E_{k1}}}}}）}^3}}$ |
11．
假设地球半径为R，地球表面的重力加速度为g，飞船在距地面高度为3R的圆轨道Ⅰ运动，到达轨道上A点点火进入椭圆轨道Ⅱ，到达轨道的近地点B再次点火进入近地轨道Ⅲ绕地球做圆周运动，不考虑飞船质量的变化，下列分析正确的是（ ）
假设地球半径为R，地球表面的重力加速度为g，飞船在距地面高度为3R的圆轨道Ⅰ运动，到达轨道上A点点火进入椭圆轨道Ⅱ，到达轨道的近地点B再次点火进入近地轨道Ⅲ绕地球做圆周运动，不考虑飞船质量的变化，下列分析正确的是（ ）| A． | 飞船在轨道Ⅱ上运行速率不可能超过7.9km/s | |
| B． | 飞船在轨道Ⅰ上运行速率为$\sqrt{\frac{gR}{3}}$ | |
| C． | 飞船从轨道Ⅰ到轨道Ⅱ机械能增加 | |
| D． | 飞船在轨道Ⅲ绕地球运行一周所需的时间为2π$\sqrt{\frac{R}{g}}$ |