题目内容
11. 如图所示.MN是足够长的光滑绝缘水平轨道.质量为m的带正电A球,以水平速度υ0射向静止在轨道上带正电的B球,至A、B相距最近时,A球的速度变为$\frac{υ_0}{4}$,已知A、B两球始终没有接触.求:
如图所示.MN是足够长的光滑绝缘水平轨道.质量为m的带正电A球,以水平速度υ0射向静止在轨道上带正电的B球,至A、B相距最近时,A球的速度变为$\frac{υ_0}{4}$,已知A、B两球始终没有接触.求:(1)B球的质量;
(2)A、B两球相距最近时,两球组成的电势能增量.
分析 (1)A、B组成的系统动量守恒,当两球相距最近时具有共同速度由动量守恒求解
(2)根据能量守恒系统求解最大电势
解答 解:(1)A、B组成的系统动量守恒,当两球相距最近时具有共同速度v,由动量守恒:
mv0=(m+mB)$\frac{{v}_{0}}{4}$
解得:mB=3m
(2)运动过程中,根据能量守恒定律得:
$△{E}_{P}=\frac{1}{2}m{{v}_{0}}^{2}-\frac{1}{2}×(m+{m}_{B}){v}^{2}$=$\frac{3}{8}m{{v}_{0}}^{2}$
答:(1)B球的质量为3m;
(2)A、B两球相距最近时,两球组成的电势能增量为$\frac{3}{8}m{{v}_{0}}^{2}$.
点评 解决该题关键要掌握系统动量守恒和能量守恒的应用,知道AB两球运动过程中,系统不受外力,明确临界条件,应用机械能守恒定律、动量守恒定律、能量守恒定律处理这类问题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
19.如图所示,一小孩从滑梯上由静止开始加速滑下,在这一过程中( )

| A. | 小孩的惯性变大 | B. | 小孩处于失重状态 | ||
| C. | 小孩处于超重状态 | D. | 小孩的机械能守恒 |
3.下列单位中属于国际单位制(SI)基本单位的是( )
| A. | 千克 | B. | 千米 | C. | 千焦 | D. | 千帕 |
1.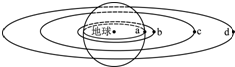 四颗地球卫星a、b、c、d的排列位置如图所示,其中a是静止在地球赤道上还未发射的卫星,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,关于四颗卫星下列说法正确的是( )
四颗地球卫星a、b、c、d的排列位置如图所示,其中a是静止在地球赤道上还未发射的卫星,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,关于四颗卫星下列说法正确的是( )
 四颗地球卫星a、b、c、d的排列位置如图所示,其中a是静止在地球赤道上还未发射的卫星,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,关于四颗卫星下列说法正确的是( )
四颗地球卫星a、b、c、d的排列位置如图所示,其中a是静止在地球赤道上还未发射的卫星,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,关于四颗卫星下列说法正确的是( )| A. | c相对于b静止 | B. | 相同时间内b转过的弧长最长 | ||
| C. | a的向心加速度最大 | D. | d的运行周期可能是23 h |
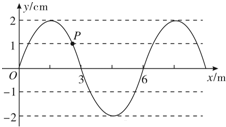 一列简谐横波沿x轴方向传播,在t=0时刻的波形如图所示,t=0.1s时,波形上P点的速度恰好第一次达到与t=0时刻的速度等值反向.若波沿x轴正方向传播,则波速v=20m/s;若波沿x轴负方向传播,则波速v=30m/s.
一列简谐横波沿x轴方向传播,在t=0时刻的波形如图所示,t=0.1s时,波形上P点的速度恰好第一次达到与t=0时刻的速度等值反向.若波沿x轴正方向传播,则波速v=20m/s;若波沿x轴负方向传播,则波速v=30m/s.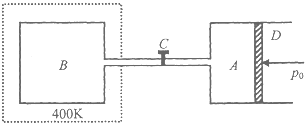 如图所示,水平放置的气缸A和容积为VB=3.6L的容器B,由一容积可忽略不计的长细管经阀门C相连,气缸A内有一活塞D,它可以无摩擦地在气缸内滑动,A放在温度恒为T1=300K,压强为p0=1.0×105Pa的大气中,B浸在T2=400K的恒温槽内,B的器壁导热性能良好,开始时C是关闭的,A内装有温度为T1=300K,体积为VA=2.4L的气体,B内没有气体,打开阀门C,使气体由A流入B,等到活塞D停止移动一段时间后,求以下两种情况下气体的体积和压强.
如图所示,水平放置的气缸A和容积为VB=3.6L的容器B,由一容积可忽略不计的长细管经阀门C相连,气缸A内有一活塞D,它可以无摩擦地在气缸内滑动,A放在温度恒为T1=300K,压强为p0=1.0×105Pa的大气中,B浸在T2=400K的恒温槽内,B的器壁导热性能良好,开始时C是关闭的,A内装有温度为T1=300K,体积为VA=2.4L的气体,B内没有气体,打开阀门C,使气体由A流入B,等到活塞D停止移动一段时间后,求以下两种情况下气体的体积和压强.