题目内容
【题目】如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,轨道的压力恰好为零,则小球落地点C距A处多远?小球冲上轨道前的速度是多大?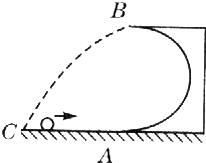
【答案】解:由题意知,当小球在B点时由重力提供向心力,可得:mg=m ![]() ,
,
所以 vB= ![]()
小球离开B点后做平抛运动,则有:
水平方向有:x=vBt
竖直方向有:2R= ![]() ,得:t=2
,得:t=2 ![]() ,
,
联立解得:小球落地点C到A点的距离:x=vBt= ![]() ×2
×2 ![]() =2R.
=2R.
小球从A点到B点过程,机械能守恒,以A点所在水平面为零势能参考面:
![]() =
= ![]() +mg2R
+mg2R
由以上方程联立解得:vA= ![]()
答:小球落地点C距A处2R,小球冲上轨道前的速度是 ![]() .
.
【解析】经过分析可知,当小球在B点时由重力提供向心力,可以求出通过B点的速度大小,再对小球进行受力分析可知,从A到B的过程中,只有重力做功,物体的机械能守恒,再对C到B的过程中运用机械能守恒定律可求得A点的速度大小,从C点飞出以后,小球做平抛运动,根据平抛运动的规律可以求出C到A的距离。

练习册系列答案
相关题目