题目内容
如图所示，水平细杆上套一环A，环A与球B间用一不可伸长轻质绳相连，质量分别为m1和m2，出于B球受到水平风力作用，A与B球一起向右匀速运动．已知绳与竖直方向的夹角为θ，则下列说法中正确的是（ ）
| A．B球受到风力为mBgtanθ | ||
| B．风力增大时，轻质绳对B球的拉力保持不变 | ||
| C．杆对A球的支持力随着风的增加而增加 | ||
D．A球与水平细杆间的动摩擦因数为
|
对球B受力分析，受重力、拉力和水平风力，如图
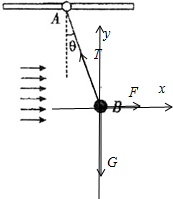
根据共点力平衡条件，有
F-Tsinθ=0
Tcosθ-mBg=0
解得
F=mBgtanθ，故A正确；
T=
T=
故绳子的拉力随风力的增大而增大，故B错误；
再对AB整体受力分析，受重力、水平风力、支持力和摩擦力，根据共点力平衡条件，有
F-f=0
N-（mA+mB）=0
解得
f=F=mBgtanθ
N=（mA+mB）g
故支持力与水平风力无关，故C错误；
μ=
=
，故D错误；
故选A．
根据共点力平衡条件，有
F-Tsinθ=0
Tcosθ-mBg=0
解得
F=mBgtanθ，故A正确；
T=
| mBg |
| cosθ |
T=
| (mBg) 2+F2 |
故绳子的拉力随风力的增大而增大，故B错误；
再对AB整体受力分析，受重力、水平风力、支持力和摩擦力，根据共点力平衡条件，有
F-f=0
N-（mA+mB）=0
解得
f=F=mBgtanθ
N=（mA+mB）g
故支持力与水平风力无关，故C错误；
μ=
| f |
| N |
| mBtanθ |
| mA+mB |
故选A．
练习册系列答案
相关题目
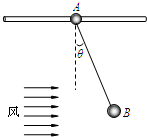如图所示，水平细杆上套一环A，环A与球B间用一轻质绳相连，质量分别为mA、mB，由于B球受到风力作用，A与B球一起向右匀速运动．已知细绳与竖直方向的夹角为θ．则下列说法中正确的是（ ）
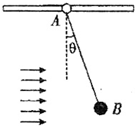（2013?岳阳二模）如图所示，水平细杆上套一环A，环A与球B间用一不可伸长轻质绳相连，质量分别为m1和m2，出于B球受到水平风力作用，A与B球一起向右匀速运动．已知绳与竖直方向的夹角为θ，则下列说法中正确的是（ ）
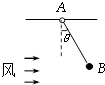（2010?山西模拟）如图所示，水平细杆上套一环A，环A与B球间用一轻绳相连，质量分别为mA、mB．由于B球受到风力作用，环A与B球一起向右匀速运动．已知细绳与竖直方向的夹角为θ．则下列说法中正确的是（ ）
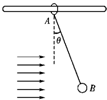如图所示，水平细杆上套一环A，环A与球B间用一轻质绳相连，质量分别为mA、mB，由于球B受到风力作用，环A与球B一起向右做匀速运动．已知细绳与竖直方向的夹角为θ，则下列说法中正确的是（ ）