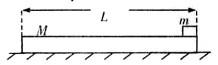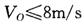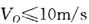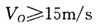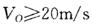题目内容
如图所示,光滑斜面CA、DA、EA都以AB为底边。三个斜面的倾角分别为75°、45°、30°。物体分别沿三个斜面由顶端从静止滑到底端,下面说法中正确的是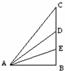
A.物体沿DA滑到底端时具有最大速率
B.物体沿EA滑到底端所需时间最短
C.物体沿CA下滑,加速度最大
D.物体沿DA滑到底端所需时间最短
CD
解析试题分析:根据动能定理得,mgh=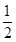 mv2.知高度越高,到达底端的速度越大.故A错误.加速度a=gsinθ,倾角越大,加速度越大,运动的位移x=
mv2.知高度越高,到达底端的速度越大.故A错误.加速度a=gsinθ,倾角越大,加速度越大,运动的位移x=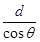 ,根据
,根据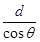 =
=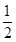 at2得,t=
at2得,t=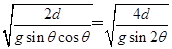 ,知当θ=45°时,下滑时间最短.故B错误,C、D正确.
,知当θ=45°时,下滑时间最短.故B错误,C、D正确.
考点:本题考查动能定理、牛顿运动定律、匀变直线运动规律。

如图所示,圆柱形的仓库内有三块长度不同的滑板aO、bO、cO,其下端都固定于底部圆心O,而上端则搁在仓库侧壁上,三块滑板与水平面的夹角依次是30°、45°、60°.若有三个小孩同时从a、b、c处开始下滑(忽略阻力),则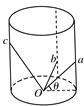
| A.a处小孩最先到O点 | B.b处小孩最先到O点 |
| C.c处小孩最先到O点 | D.三个小孩同时到O点 |
2009年9月28日,甬台温高速铁路客运列车正式开通,结束了我市没有铁路的历史.假设列车在某段距离中做匀加速直线运动,速度由10m/s增加到50m/s时位移为x.则当速度由10m/s增加到30m/s时,它的位移是( )
| A.x/3 | B.x/2 | C.2x | D.3x |
物体做匀加速直线运动时,下列说法中正确的是:( )
| A.速度总是与时间成正比. |
| B.速度的增加量与时间的比值均匀增大. |
| C.任意两个连续相等的时间间隔里的位移之差一定相等. |
| D.在任意时间段内的平均速度一定是(v0+ vt)/2. |
一辆汽车正在做匀加速直线运动,计时之初,速度为6 m/s,运动28 m后速度增加到8 m/s,则( )
| A.这段运动所用时间是4 s |
| B.这段运动的加速度是3.5 m/s2 |
| C.自开始计时起,两秒末的速度是7 m/s |
D.从开始计时起,经过14 m处的速度是5 m/s m/s |
如图所示,以8m/s匀速行驶的汽车即将通过路口,绿灯还有2 s将熄灭,此时汽车距离停车线18m。该车加速时最大加速度大小为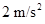 ,减速时最大加速度大小为
,减速时最大加速度大小为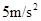 。此路段允许行驶的最大速度为
。此路段允许行驶的最大速度为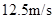 ,下列说法中正确的有( )
,下列说法中正确的有( )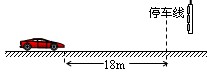
| A.如果立即做匀加速运动,在绿灯熄灭前汽车可能通过停车线 |
| B.如果立即做匀加速运动,在绿灯熄灭前通过停车线汽车一定超速 |
| C.如果立即做匀减速运动,在绿灯熄灭前汽车一定不能通过停车线 |
D.如果距停车线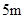 处减速,汽车能停在停车线处 处减速,汽车能停在停车线处 |
如图所示,几条足够长的光滑直轨道与水平面成不同角度,从P点以大小不同的初速度沿各轨道发射小球,若各小球恰好在相同的时间内达到各自的最高点,则各小球最高点的位置
| A.在同一水平线上 | B.在同一竖直线上 |
| C.在同一抛物线上 | D.在同一圆周上 |
 ,A、B球受到相同大小的空气阻力,两球与地面碰撞均为弹性碰撞,则以下说法正确的是:( )
,A、B球受到相同大小的空气阻力,两球与地面碰撞均为弹性碰撞,则以下说法正确的是:( )
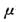 =0.8.若要使木板获得的速度不大于2m/S,木块的初速度V0应满足的条件为(g取10m/s2)( )
=0.8.若要使木板获得的速度不大于2m/S,木块的初速度V0应满足的条件为(g取10m/s2)( )