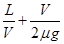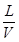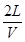题目内容
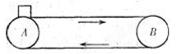
如图所示，质量M=4kg长为L=1Om的木板停放在光滑水平面上，另一不计长度质量m=1kg的木块以某一速度从右端滑上木板，木板与木块间的动摩擦因数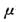
=0．8．若要使木板获得的速度不大于2m/S，木块的初速度V0应满足的条件为（g取10m/s2）（ ）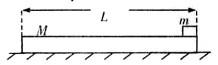
A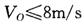． | B． |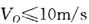
C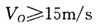． | D． |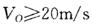
BC
解析试题分析: 木块在木板上滑动时，木块的加速度a1=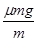
=8m/s，木板的加速度a2=
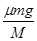= m/s，若木块最终从左端离开木板，则此过程中木板一直做匀加速运动，木块离开时，木板速度最大，则有v2≤2m/s，所以t≤
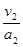=1s，木块一直做匀减速运动，则有：x木块-x木板=10m
即v0t+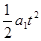
-
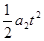=10m，带入数据解得：v0≥15m/s
若木块先减速后和木板一起匀速运动，根据动量守恒定律得：
mv0=（m+M）v，解得：v0=5v，因为v≤2m/s，所以v0≤10m/s。故选BC
考点：牛顿第二定律；动量守恒定律；匀变速直线运动规律。
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案（6分）一物体沿固定斜面从静止开始向下运动，经过时间
滑至斜面底端.已知在物体运动过程中物体所受的摩擦力恒定.题10图1中描述的是物体运动过程中，物体的物理量与时间的关系图，横坐标表示运动的时间，则纵坐标可能表示的是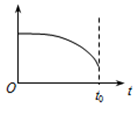
| A．物体所受的合外力 | B．物体的速度 |
| C．物体的重力势能 | D．物体的机械能 |
酒后驾驶会导致许多安全隐患，是因为驾驶员的反应时间变长，反应时间是指驾驶员从发现情况到采取制动的时间。下表中“思考距离”是指驾驶员从发现情况到采取制动的时间内汽车行驶的距离，“制动距离”是指驾驶员从发现情况到汽车停止行驶的距离（假设汽车制动时的加速度大小都相同）。
| 速度（m/s） | 思考距离/m | 制动距离/m | ||
| 正常 | 酒后 | 正常 | 酒后 | |
| 15 | 7.5 | 15.0 | 22.5 | 30.0 |
| 20 | 10.0 | 20.0 | 36.7 | 46.7 |
| 25 | 12.5 | 25.0 | 54.2 | x |
A．驾驶员酒后反应时间比正常情况下多0.5s
B．若汽车以20m/s的速度行驶时，发现前方40m处有险情，酒后驾驶不能安全停车
C．汽车制动时，加速度大小为10m/s2
D．表中x为66.7
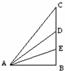
某同学探究小球沿光滑斜面顶端下滑至底端的运动规律，现将两质量相同的小球同时从斜面的顶端释放，在甲、乙图的两种斜面中，通过一定的判断分析，你可以得到的正确结论是( )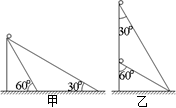
| A．甲图中小球在两个斜面上运动的时间相同 |
| B．甲图中小球下滑至底端的速度大小与方向均相同 |
| C．乙图中小球在两个斜面上运动的时间相同 |
| D．乙图中小球下滑至底端的速度大小相同 |
如图所示，AB1、AB2是两个光滑斜面。使一个物体先后从A点由静止开始沿两个斜面滑下，分别滑到斜面底端B1和B2处，则比较物体在两个斜面上滑动的情况，下面结论正确的是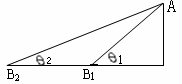
| A．物体沿AB1斜面下滑的加速度大 |
| B．物体沿AB1斜面滑到底端用的时间短 |
| C．物体沿AB1斜面滑到底端时的速度大 |
| D．物体沿两个斜面到底端时的速度一样大 |
一架飞机在地面从静止加速到刚离开地面的过程中，在30秒内速度由0增加到324km/h，若认为飞机加速过程是匀加速的，则：（ ）
| A．飞机的加速度是10.8m/s2 |
| B．飞机的平均速度为162m/s |
| C．飞机的跑道长至少是1300m |
| D．飞机在15s时的瞬时速度是45m/s |
关于匀变速直线运动的下列说法，正确的是( )
| A．匀加速直线运动的速度一定与时间成正比 |
| B．匀减速直线运动就是加速度为负值的运动 |
| C．匀变速直线运动的速度随时间均匀变化 |
| D．速度先减小再增大的运动一定不是匀变速直线运动 |