题目内容
14.有一横截面积为S的铜导线,流经其中的电流为I,设每单位体积的导线有n个自由电子,电子电量为e,此时电子的定向转动速度为v,在△t时间内,通过导体横截面的自由电子数目可表示为( )| A. | nvS△t | B. | nv△t | C. | $\frac{I△t}{n}$ | D. | $\frac{I△t}{Se}$ |
分析 根据电流的微观表达式I=nqvs,求出在△t时间内通过导体横截面的自由电子的电量,每个电子的电量为q,再确定通过导体横截面的自由电子的数目.
解答 解:根据电流的微观表达式I=nqvS,在△t时间内通过导体横截面的自由电子的电量Q=I△t,
则在△t时间内,通过导体横截面的自由电子的数目为n=$\frac{Q}{q}=\frac{I△t}{q}$,
将I=nevS代入得n=$\frac{Q}{q}=\frac{nqvS△t}{q}$=nvS△t,故A正确,BCD错误.
故选:A
点评 本题考查电流的微观表达式和定义式综合应用的能力,电流的微观表达式I=nqvs,是联系宏观与微观的桥梁,常常用到.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
2.质量为m的小球A在光滑水平面上以速度v0与质量为2m的静止小球发生碰撞,碰撞后,A球的速度大小变为原来的$\frac{1}{3}$,则碰撞后B球的速度可能是( )
| A. | $\frac{{v}_{0}}{3}$ | B. | $\frac{2{v}_{0}}{3}$ | C. | $\frac{4{v}_{0}}{9}$ | D. | $\frac{5{v}_{0}}{9}$ |
9.酒后驾驶会导致许多安全隐患,是因为驾驶员的反应时间变长,反应时间是指驾驶员从发现情况到采取制动的时间.表中“思考距离”是指驾驶员从发现情况到采取制动的时间内汽车行驶的距离,“制动距离”是指驾驶员从发现情况到汽车停止行驶的距离(假设汽车制动时的加速度大小都相同).
分析表,求解下列问题
(1)驾驶员酒后反应时间比正常情况下多用多少时间?
(2)若汽车以20m/s的速度行驶时,发现前方40m处有险情,判断酒后驾驶能不能安全停车.
| 速度(m/s) | 思考距离/m | 制动距离/m | ||
| 正常 | 酒后 | 正常 | 酒后 | |
| 15 | 7.5 | 15.0 | 22.5 | 30.0 |
(1)驾驶员酒后反应时间比正常情况下多用多少时间?
(2)若汽车以20m/s的速度行驶时,发现前方40m处有险情,判断酒后驾驶能不能安全停车.
19. 如图所示,A、B是两个架在绝缘支座上的金属球,都不带电,中间用导线连接,现用一带负电的小球C靠近A,用手摸一下A球,再撤去导线,然后移走C球,则A、B带电情况( )
如图所示,A、B是两个架在绝缘支座上的金属球,都不带电,中间用导线连接,现用一带负电的小球C靠近A,用手摸一下A球,再撤去导线,然后移走C球,则A、B带电情况( )
 如图所示,A、B是两个架在绝缘支座上的金属球,都不带电,中间用导线连接,现用一带负电的小球C靠近A,用手摸一下A球,再撤去导线,然后移走C球,则A、B带电情况( )
如图所示,A、B是两个架在绝缘支座上的金属球,都不带电,中间用导线连接,现用一带负电的小球C靠近A,用手摸一下A球,再撤去导线,然后移走C球,则A、B带电情况( )| A. | A球带正电,B球带负电 | B. | A球带正电,B球不带电 | ||
| C. | A球不带电,B球带负电 | D. | 以上说法都不正确 |
3.两个完全相同的金属小球,带电量之比为1:5,两带电小球可视为点电荷,在真空中相距为r时,相互作用力为F;若把它们接触后再放回原处,则它们之间的相互作用力可能为( )
| A. | $\frac{9}{5}F$ | B. | $\frac{5}{9}F$ | C. | $\frac{3}{5}F$ | D. | $\frac{4}{5}F$ |
4.质量和电荷量不同的带电粒子,在电场中由静止开始经相同电压加速后( )
| A. | 比荷大的粒子速度大,电荷量大的粒子动能大 | |
| B. | 比荷大的粒子动能大,电荷量大的粒子速度大 | |
| C. | 比荷大的粒子速度和动能都大 | |
| D. | 电荷量大的粒子速度和动能都大 |
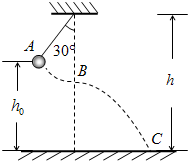 如图所示,让小球从图中的位置A由静止开始下摆,正好摆到最低点B时摆线被拉断,设摆线长l=1.6m,悬点到地面的高度为h=6.6m,不计空气阻力,求摆球落地时的速度.
如图所示,让小球从图中的位置A由静止开始下摆,正好摆到最低点B时摆线被拉断,设摆线长l=1.6m,悬点到地面的高度为h=6.6m,不计空气阻力,求摆球落地时的速度. 如图为一列沿x轴正方向传播的简谐波在t=0时刻的波形图,已知波速为10m/s,则图中P质点的振动方程为y=10sin5πt(cm)×(判断对错)
如图为一列沿x轴正方向传播的简谐波在t=0时刻的波形图,已知波速为10m/s,则图中P质点的振动方程为y=10sin5πt(cm)×(判断对错)