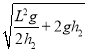Question

【题目】如图所示，一辆小车静止在水平地面上，车内固定着一个倾角为60°的光滑斜面OA，光滑挡板OB可绕转轴O在竖直平面内转动。现将一重为G的圆球放在斜面与挡板之间，挡板与水平面的夹角θ＝60°。下列说法正确的是（ ）

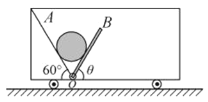
A.若保持挡板不动，则球对斜面的压力大小为G

B.若挡板从图示位置顺时针方向缓慢转动60°，则球 对斜面的压力先减小后增大

C.若挡板从图示位置顺时针方向缓慢转动30°，则球 对挡板的压力先减小后增大

D.保持θ＝60°不变，使小车水平向左加速运动，则球对斜面OA的压力可能为零

Answer 1

【答案】AD

【解析】

考查受力分析，动态平衡，力的三角形定则。

A．若保持挡板不动，球受力平衡，对球受力分析，正交分解可得：

解得，由牛顿第三定律可得，球对斜面的压力大小为G，A正确；

B．对球受力

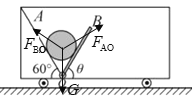
由三角形定则，旋转过程中，力的变化如图所示：

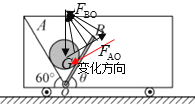
若挡板从图示位置顺时针方向缓慢转动60°过程中，一直减小，B错误；

C． 挡板从图示位置顺时针方向缓慢转动30°时，刚好与垂直，此时最小，则球对挡板的压力一直减小，C错误；

D．保持θ＝60°不变，若球对斜面OA的压力为零，则有：

解得，即当小车水平向左加速运动的加速度大小为时，球对斜面OA的压力为0，D正确。

故选AD 。