题目内容
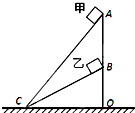
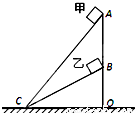
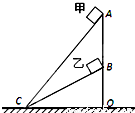
 如图所示,A、C和B、C是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物体在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别是m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C的过程中克服摩擦力做的功分别是W1、W2,所需时间分别是t1、t2.甲、乙滑至底端C时速度分别是v1、v2,动能分别是EK1、EK2,则( )
如图所示,A、C和B、C是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物体在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别是m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C的过程中克服摩擦力做的功分别是W1、W2,所需时间分别是t1、t2.甲、乙滑至底端C时速度分别是v1、v2,动能分别是EK1、EK2,则( )分析:应用动能定理求出物体到达底端的动能,然后比较动能大小,根据动能的计算公式求出物体的速度,然后比较大小;由功的计算公式求出克服摩擦力所做的功,然后比较功的大小;由牛顿第二定律与运动学公式求出物体的运动时间,然后比较时间大小.
解答:解:A、设斜面的倾角为θ,斜面水平长度为L,由动能定理得:mgLtanθ-μmgcosθ
=EK1-0,EK1=mgL(tanθ-μ),
m1<m2,θ1>θ2,无法判断两物体动能大小,故A错误;
B、EK1=mgL(tanθ-μ)=
mv2,v=
,θ1>θ2,v1>v2,故B正确;
C、克服摩擦力做的功W=μmgcosθ×
=μmgL,∵m1<m2,∴W1<W2,故C正确;
D、由牛顿第二定律得:mgsinθ-μmgcosθ=ma,
=
at2,t=
,θ1>θ2,则t1>t2,故D错误;
故选BC.
| L |
| cosθ |
m1<m2,θ1>θ2,无法判断两物体动能大小,故A错误;
B、EK1=mgL(tanθ-μ)=
| 1 |
| 2 |
| 2gL(tanθ-μ) |
C、克服摩擦力做的功W=μmgcosθ×
| L |
| cosθ |
D、由牛顿第二定律得:mgsinθ-μmgcosθ=ma,
| L |
| cosθ |
| 1 |
| 2 |
|
故选BC.
点评:熟练应用动能定理、功的计算公式、牛顿第二定律、运动学公式即可正确解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目