题目内容
 (2012?徐州一模)适合选修3-4模块的考生
(2012?徐州一模)适合选修3-4模块的考生(1)下列说法中正确的是
C
C
A.光的偏振现象证明了光波是纵波
B.在发射无线电波时,需要进行调谐和解调
C.在白炽灯的照射下从两块捏紧的玻璃板表面看到彩色条纹,这是光的干涉现象
D.考虑相对论效应,一条沿自身长度方向运动的杆其长度总比杆静止时的长度长
(2)如图1所示为一列简谐横波t=0时刻的波动图象,已知波沿x轴正方向传播,波速大小为0.4m/s.则在图示时刻质点a、b所受的回复力大小之比为
2:1
2:1
,此时刻起,质点c的振动方程是:y=15cos10πt
y=15cos10πt
cm.(3)如图2所示的装置可以测量棱镜的折射率,ABC表示待测直角棱镜的横截面,棱镜的顶角为α,紧贴直角边AC是一块平面镜,一光线SO射到棱镜的AB面上,适当调整SO的方向,当SO与AB成β角时,从AB面射出的光线与SO重合,在这种情况下可测得棱镜的折射率n=
| cosβ |
| sinα |
| cosβ |
| sinα |
分析:(1)光的振现象证明了光波是横波;调谐和解调是接收电磁波时的操作步骤,发射电磁波时需调制;在白炽灯的照射下从两块捏紧的玻璃板表面看到彩色条纹,是光在空气膜上下表面反射后叠加产生的干涉条纹;根据长度的相对性判断长度的变化.
(2)根据F=-kx,通过偏离平衡位置的位移求出回复力大小之比,根据波长和波速求出周期,根据振动方程的表达式写出c点的振动方程.
(3)根据几何关系得出入射角和折射角,通过折射定律求出棱镜的折射率.
(2)根据F=-kx,通过偏离平衡位置的位移求出回复力大小之比,根据波长和波速求出周期,根据振动方程的表达式写出c点的振动方程.
(3)根据几何关系得出入射角和折射角,通过折射定律求出棱镜的折射率.
解答:解:(1)A、光的偏振现象证明了光波是横波.故A错误.
B、在发射无线电波时,需要进行调制.故B错误.
C、在白炽灯的照射下从两块捏紧的玻璃板表面看到彩色条纹,这是光的干涉现象.故C正确.
D、考虑相对论效应,一条沿自身长度方向运动的杆其长度总比杆静止时的长度短.故D错误.
故选C.
(2)根据F=-kx知,a、b两质点偏离平衡位置的距离之比为2:1,则回复力之比为2:1.波长λ=0.08m,则T=
=
s=0.2s.ω=
=10πrad/s,
质点c初始时刻处于正向最大位移处,根据y=Acosωt=15cos10πtcm.
(3)当SO与AB成β角时,从AB面射出的光线与SO重合,知在AB面上的折射光线与AC面垂直,根据几何关系得,入射角为90°-β,折射角为α,根据折射定律得,
n=
=
.
故答案为:(1)C
(2)2:1,y=15cos10πt
(3)
.
B、在发射无线电波时,需要进行调制.故B错误.
C、在白炽灯的照射下从两块捏紧的玻璃板表面看到彩色条纹,这是光的干涉现象.故C正确.
D、考虑相对论效应,一条沿自身长度方向运动的杆其长度总比杆静止时的长度短.故D错误.
故选C.
(2)根据F=-kx知,a、b两质点偏离平衡位置的距离之比为2:1,则回复力之比为2:1.波长λ=0.08m,则T=
| λ |
| v |
| 0.08 |
| 0.4 |
| 2π |
| T |
质点c初始时刻处于正向最大位移处,根据y=Acosωt=15cos10πtcm.
(3)当SO与AB成β角时,从AB面射出的光线与SO重合,知在AB面上的折射光线与AC面垂直,根据几何关系得,入射角为90°-β,折射角为α,根据折射定律得,
n=
| sin(90°-β) |
| sinα |
| cosβ |
| sinα |
故答案为:(1)C
(2)2:1,y=15cos10πt
(3)
| cosβ |
| sinα |
点评:本题考查选修3-4中的内容,侧重与几何光学问题和波动与振动问题,关键要熟悉教材,牢记基本概念和基本规律.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 (2012?徐州一模)如图所示,在真空中有两个带正电的点电荷,分别置于P、Q两点,P处正点电荷的电荷量大于Q处点电荷的电荷量,A、B为P、Q连线的中垂线上的两点,现将一负电荷q 由A点沿中垂线移动到B点,在此过程中,下列说法正确的是( )
(2012?徐州一模)如图所示,在真空中有两个带正电的点电荷,分别置于P、Q两点,P处正点电荷的电荷量大于Q处点电荷的电荷量,A、B为P、Q连线的中垂线上的两点,现将一负电荷q 由A点沿中垂线移动到B点,在此过程中,下列说法正确的是( )
 (2012?徐州一模)如图所示,在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆AC,其下端(C端)距地面高度h=0.8m.有一质量500g的带电小环套在直杆上,正以某一速度沿杆匀速下滑,小环离杆后正好通过C端的正下方P点处.(g=10m/s2)求:
(2012?徐州一模)如图所示,在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆AC,其下端(C端)距地面高度h=0.8m.有一质量500g的带电小环套在直杆上,正以某一速度沿杆匀速下滑,小环离杆后正好通过C端的正下方P点处.(g=10m/s2)求: (2012?徐州一模)如图所示,三根通电长直导线P、Q、R互相平行,垂直纸面放置,其间距均为a,电流强度均为I,方向垂直纸面向里(已知电流为I的长直导线产生的磁场中,距导线r处的磁感应强度B=kI/r,其中k为常数).某时刻有一电子(质量为m、电量为e)正好经过原点O,速度大小为v,方向沿y轴正方向,则电子此时所受磁场力为( )
(2012?徐州一模)如图所示,三根通电长直导线P、Q、R互相平行,垂直纸面放置,其间距均为a,电流强度均为I,方向垂直纸面向里(已知电流为I的长直导线产生的磁场中,距导线r处的磁感应强度B=kI/r,其中k为常数).某时刻有一电子(质量为m、电量为e)正好经过原点O,速度大小为v,方向沿y轴正方向,则电子此时所受磁场力为( )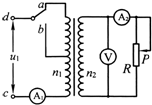 (2012?徐州一模)如图所示,理想变压器原、副线圈的匝数比为10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,除R以外其余电阻不计.从某时刻开始在原线圈c、d两端加上
(2012?徐州一模)如图所示,理想变压器原、副线圈的匝数比为10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,除R以外其余电阻不计.从某时刻开始在原线圈c、d两端加上