题目内容
 (2012?徐州一模)如图所示,在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆AC,其下端(C端)距地面高度h=0.8m.有一质量500g的带电小环套在直杆上,正以某一速度沿杆匀速下滑,小环离杆后正好通过C端的正下方P点处.(g=10m/s2)求:
(2012?徐州一模)如图所示,在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆AC,其下端(C端)距地面高度h=0.8m.有一质量500g的带电小环套在直杆上,正以某一速度沿杆匀速下滑,小环离杆后正好通过C端的正下方P点处.(g=10m/s2)求:(1)小环带何种电荷?离开直杆后运动的加速度大小和方向.
(2)小环从C运动到P过程中的动能增量.
(3)小环在直杆上匀速运动速度的大小υ0.
分析:小环在置于电场中的倾斜的光滑绝缘直杆上匀速下滑,由共点力平衡结合重力与支持力方向可判断出电场力方向,又由电场强度的方向可得出电荷的电性.当小环离开直杆后,仅少了支持力.则此时的合力就是由重力与电场力提供,由牛顿第二定律可求出离开后的加速度大小与方向.小环离开直杆后,所受合力恰与速度方向垂直,因此做的类平抛运动.当小环从C到P过程中,电场力做功刚好为零,动能的变化完全由重力做功引起.当求小环离开直杆的速度时,仅从离开前无法入手,而离开后做类平抛运动,所以利用垂直于杆的方向与沿杆的方向的位移可求出小环的抛出速度.
解答:解:(1)对带电小环受力分析
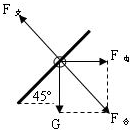
因带电小环匀速下滑,加之电场强度水平向左,所以小环带负电.
由几何关系可知,小环所受电场力与重力大小相等.则小环离开直杆后所受的合外力大小为:F合=
mg
由牛顿第二定律可得:a=
g=10
m/s2
方向垂直于杆向下(或与水平方向成45°角斜向下).
(2)设小环从C运动到P过程中动能的增量为△Ek.由动能定理有:WG+WE=△Ek
∵电场力做功为零WE=0
∴△Ek=WG=mgh=4J
(3)小环离开杆做类平抛运动.如图所示建立坐标x、y轴
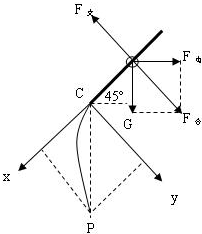
垂直于杆方向做匀加速运动:y=
at2=
h
平行于杆方向做匀速运动:x=υ0t=
h
解得:υ0=2m/s

因带电小环匀速下滑,加之电场强度水平向左,所以小环带负电.
由几何关系可知,小环所受电场力与重力大小相等.则小环离开直杆后所受的合外力大小为:F合=
| 2 |
由牛顿第二定律可得:a=
| 2 |
| 2 |
方向垂直于杆向下(或与水平方向成45°角斜向下).
(2)设小环从C运动到P过程中动能的增量为△Ek.由动能定理有:WG+WE=△Ek
∵电场力做功为零WE=0
∴△Ek=WG=mgh=4J
(3)小环离开杆做类平抛运动.如图所示建立坐标x、y轴

垂直于杆方向做匀加速运动:y=
| 1 |
| 2 |
| ||
| 2 |
平行于杆方向做匀速运动:x=υ0t=
| ||
| 2 |
解得:υ0=2m/s
点评:考查带电粒子在电场与重力场共同作用下的运动,在直杆的束缚下的匀速直线运动与没有束缚下的类平抛运动.重点突出对研究对象的受力分析与运动分析,结合运动学公式、牛顿第二定律与动能定理等物理规律.

练习册系列答案
相关题目
 (2012?徐州一模)如图所示,在真空中有两个带正电的点电荷,分别置于P、Q两点,P处正点电荷的电荷量大于Q处点电荷的电荷量,A、B为P、Q连线的中垂线上的两点,现将一负电荷q 由A点沿中垂线移动到B点,在此过程中,下列说法正确的是( )
(2012?徐州一模)如图所示,在真空中有两个带正电的点电荷,分别置于P、Q两点,P处正点电荷的电荷量大于Q处点电荷的电荷量,A、B为P、Q连线的中垂线上的两点,现将一负电荷q 由A点沿中垂线移动到B点,在此过程中,下列说法正确的是( )
 (2012?徐州一模)如图所示,三根通电长直导线P、Q、R互相平行,垂直纸面放置,其间距均为a,电流强度均为I,方向垂直纸面向里(已知电流为I的长直导线产生的磁场中,距导线r处的磁感应强度B=kI/r,其中k为常数).某时刻有一电子(质量为m、电量为e)正好经过原点O,速度大小为v,方向沿y轴正方向,则电子此时所受磁场力为( )
(2012?徐州一模)如图所示,三根通电长直导线P、Q、R互相平行,垂直纸面放置,其间距均为a,电流强度均为I,方向垂直纸面向里(已知电流为I的长直导线产生的磁场中,距导线r处的磁感应强度B=kI/r,其中k为常数).某时刻有一电子(质量为m、电量为e)正好经过原点O,速度大小为v,方向沿y轴正方向,则电子此时所受磁场力为( )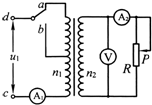 (2012?徐州一模)如图所示,理想变压器原、副线圈的匝数比为10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,除R以外其余电阻不计.从某时刻开始在原线圈c、d两端加上
(2012?徐州一模)如图所示,理想变压器原、副线圈的匝数比为10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,除R以外其余电阻不计.从某时刻开始在原线圈c、d两端加上