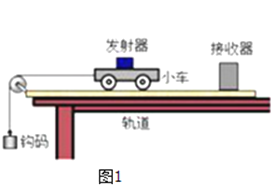
题目内容
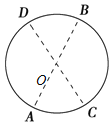
【题目】如图,立柱固定于光滑水平面上O点,质量为M的小球a向右运动,与静止于Q点的质量为m的小球b发生弹性碰撞,碰后a球立即向左运动,b球与立柱碰撞能量不损失,所有碰撞时间均不计,b球恰好在P点追到a球,Q点为OP间中点,则a、b球质量之比M:![]()
![]()
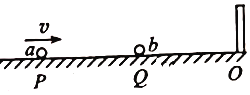
A. 3:5 B. 1:3 C. 2:3 D. 1:2
【答案】A
【解析】
根据碰后再次相遇的路程关系,求出两球碰后的速度大小之比。根据碰撞过程中动量、能量守恒列方程即可求出a、b球质量之比M:m.
设a、b两球碰后速度大小分别为v1、v2.
由题有:b球与挡板发生弹性碰撞后恰好在P点追上甲,则从碰后到相遇a、b球通过的路程之比为:s1:s2=1:3
根据s=vt得:v2=3v1
以水平向右为正方向,两球发生弹性碰撞,由动量守恒定律得:Mv0=M(-v1)+mv2
由机械能守恒定律得:![]()
解得M:m=3:5
故选A.

练习册系列答案
相关题目