题目内容
如图所示,三个质量均为m的小木块在三个质量均为M、倾角均为α的固定锲块上下滑它们与锲块间的动摩擦因数各不相同,致使第一小木块加速下滑,第二小木块匀速下滑,第三小木块以初速υ0减速下滑.则在下滑过程中,锲块对地面的压力N1、N2、N3之间的关系为
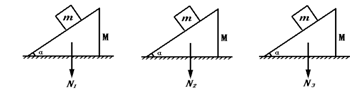

| A.N1=N2=N3 |
| B.N1>N2>N3 |
| C.N2>N1>N3 |
| D.N3>N2>N1? |
D
分析:以木块和斜面整体为研究对象,分析受力情况,作出力图,将加速度进行分解,根据牛顿第二定律得到地面对锲块的支持力与总重力的关系,再进行选择.
解答:
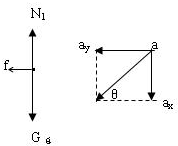
解:当木块加速下滑时,木块的加速度沿锲块向下,将木块的加速度分解为水平和竖直两个方向,如图,根据牛顿第定律得知:N1<G
 ,
,同理可得,当木块匀速下滑时,N2= G
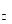 ,当木块减速时,N3>G
,当木块减速时,N3>G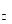 ,可见, N3>N2>N1.
,可见, N3>N2>N1.故选D
点评:本题对加速度不同的两个物体运用整体法,根据牛顿第二定律研究物体的受力情况,也可以运用超重或失重的观点进行分析.

练习册系列答案
相关题目
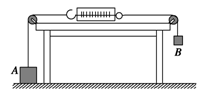
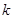 的轻质弹簧,上端固定,下端连着一质量为m的物块A,A放在托盘B上,初始时全都静止,弹簧处于自然长度,现设法控制B的运动,使A匀加速下降,用
的轻质弹簧,上端固定,下端连着一质量为m的物块A,A放在托盘B上,初始时全都静止,弹簧处于自然长度,现设法控制B的运动,使A匀加速下降,用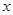 表示弹簧伸长量,用
表示弹簧伸长量,用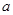 表示A的加速度,则在能保持A匀加速下降的整个过程中(始终在弹簧弹性限度内),重力加速度为g,下列说法正确的有 ( )
表示A的加速度,则在能保持A匀加速下降的整个过程中(始终在弹簧弹性限度内),重力加速度为g,下列说法正确的有 ( )
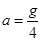 ,则弹簧最大形变量为
,则弹簧最大形变量为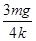
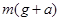
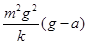

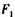 和
和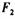 均变大
均变大 和
和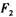 均变小
均变小 变大,
变大, 变小
变小 变小,
变小, 变大
变大