题目内容
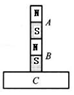
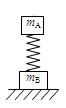
如图所示,两个完全相同的匀质光滑小球,静止在内壁光滑的半球形碗底,两球之间相互作用力的大小为P,每个小球对碗的压力大小均为F2若两小球质量不变,而半径均减小为原来、的一半,则


A.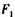 和 和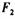 均变大 均变大 | B. 和 和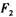 均变小 均变小 |
C. 变大, 变大, 变小 变小 | D. 变小, 变小, 变大 变大 |
B
分析:设碗对球的支持力与竖直方向的夹角为α.以其中某一个球为研究对象,分析受力,作出力图,根据平衡条件求出碗对球的支持力和另一球对它的弹力与α的关系式,根据数学分析当碗的半径逐渐增大时,α如何变化.再分析F1和F2如何变化.
解答:解: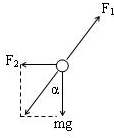 以左边的球为研究对象,作出力图,如图.设碗对球的支持力F1与竖直方向的夹角为α.根据平衡条件得, F1=
以左边的球为研究对象,作出力图,如图.设碗对球的支持力F1与竖直方向的夹角为α.根据平衡条件得, F1=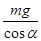 F2=mgtanα
F2=mgtanα
当碗的半径逐渐增大时,α变小,cosα变大,tanα变小
则F1变小,F2变小.
故选B
点评:本题采用的是函数法来进行动态变化分析,也可以采用极限法分析:图示位置碗对球的支持力F1大于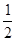 mg,F2>0,当半径增大到无穷大时,F1=
mg,F2>0,当半径增大到无穷大时,F1=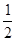 mg,F2=0,则两个力均变小.
mg,F2=0,则两个力均变小.
解答:解:
 以左边的球为研究对象,作出力图,如图.设碗对球的支持力F1与竖直方向的夹角为α.根据平衡条件得, F1=
以左边的球为研究对象,作出力图,如图.设碗对球的支持力F1与竖直方向的夹角为α.根据平衡条件得, F1=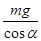 F2=mgtanα
F2=mgtanα当碗的半径逐渐增大时,α变小,cosα变大,tanα变小
则F1变小,F2变小.
故选B
点评:本题采用的是函数法来进行动态变化分析,也可以采用极限法分析:图示位置碗对球的支持力F1大于
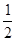 mg,F2>0,当半径增大到无穷大时,F1=
mg,F2>0,当半径增大到无穷大时,F1=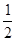 mg,F2=0,则两个力均变小.
mg,F2=0,则两个力均变小.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目