题目内容
(2012?石家庄一模)为了研究轻质弹簧的弹性势能与弹簧压缩量的关系,某实验小组的实验装置如图所示,光滑水平桌面距地面高为h,一轻质弹簧左端固定,右端与质量为m的小钢球接触,弹簧处于原长.将小球向左推,压缩弹簧一段距离后由静止释放,弹簧将小球沿水平方向推出,小球落到位于水平地面的记录纸上,留下痕迹,已知重力加速度为g
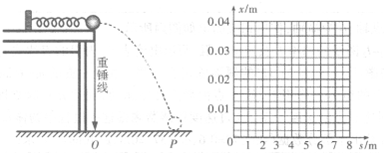
(1)某次实验测得小球的落点P到O点的距离为s,那么由理论分析得到小球释放前压缩弹簧的弹性势能Ep与h、s、mg之间的关系式为
(2)改变弹簧压缩量进行多次实验,测量数据如下表所示,请在坐标纸上做出x-s图象.
(3)由图象得出x与s的关系式为

(1)某次实验测得小球的落点P到O点的距离为s,那么由理论分析得到小球释放前压缩弹簧的弹性势能Ep与h、s、mg之间的关系式为
Ep=
| mgs2 |
| 4h |
Ep=
;| mgs2 |
| 4h |
(2)改变弹簧压缩量进行多次实验,测量数据如下表所示,请在坐标纸上做出x-s图象.
| 弹簧压缩量x/m | 0.010 | 0.015 | 0.020 | 0.025 | 0.030 | 0.035 |
| 小球飞行水平距离s/m | 2.0 | 3.0 | 4.1 | 5.9 | 6.0 | 7.0 |
x=0.005s
x=0.005s
;由实验得到弹簧弹性势能Ep与弹簧压缩量x之间的关系式为Ep=
| 104mgx2 |
| h |
Ep=
.| 104mgx2 |
| h |
分析:首先对小球的运动情况进行分析,小球离开光滑槽后做平抛运动,常用的方法是把运动沿水平和竖直方向进行分解为匀速直线运动和自由落体运动,分别进行列式可求出小球释放前压缩弹簧的弹性势能Ep与h、s和mg之间的关系式.
通过对图线的斜率进行分析和求解,可得出x和s之间的关系,结合以上的结论可得到弹簧弹性势能与弹簧压缩量x之间的关系式.
通过对图线的斜率进行分析和求解,可得出x和s之间的关系,结合以上的结论可得到弹簧弹性势能与弹簧压缩量x之间的关系式.
解答:故答案为:(1)、小钢球离开光滑槽后做平抛运动,设运动时间为t,离开光滑槽时的速度为v0.在竖直方向上是自由落体运动:
有:h=
gt2…(1)
水平方向上是匀速直线运动:
s=v0t…(2)
在弹簧推小球的过程中,机械能守恒,所以有:
Ep=
mv2…(3)
由(1)(2)(3)式联立得:
Ep=
…(4)
(2)通过描点法根据测量数据作出x-s图象.
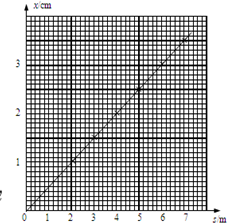
(3)、通过图象可以看出,当s=5m时,x=2.5cm,x与s图线的斜率k=0.005,
所以x与s的关系式是x=0.005s…(5)
由(4)(5)两式联立得:Ep=
故答案为:(1)Ep=
;(2)图象如图;(3)x=0.005s,Ep=
有:h=
| 1 |
| 2 |
水平方向上是匀速直线运动:
s=v0t…(2)
在弹簧推小球的过程中,机械能守恒,所以有:
Ep=
| 1 |
| 2 |
由(1)(2)(3)式联立得:
Ep=
| mgs2 |
| 4h |
(2)通过描点法根据测量数据作出x-s图象.

(3)、通过图象可以看出,当s=5m时,x=2.5cm,x与s图线的斜率k=0.005,
所以x与s的关系式是x=0.005s…(5)
由(4)(5)两式联立得:Ep=
| 104mgx2 |
| h |
故答案为:(1)Ep=
| mgs2 |
| 4h |
| 104mgx2 |
| h |
点评:该题首先是考察了平抛运动的应用,解决关于平抛运动的问题常用的方法是沿着水平和竖直两个方向进行分解,运用各方向上的运动规律进行解答.
再次是考察了应用实验数据进行绘制图线,在绘制图线时要使尽可能多的点落到直线上,并使不在直线上的点尽可能的平均分布在直线的两侧,利用x与s之间的关系求出弹簧弹性势能与弹簧压缩量x之间的关系式.
再次是考察了应用实验数据进行绘制图线,在绘制图线时要使尽可能多的点落到直线上,并使不在直线上的点尽可能的平均分布在直线的两侧,利用x与s之间的关系求出弹簧弹性势能与弹簧压缩量x之间的关系式.

练习册系列答案
相关题目
 (2012?石家庄一模)在实验精度要求不高的情况下,可利用罗盘来测量电流产生磁场的磁感应强度.具体做法是:在一根南北方向放置的直导线的正下方10cm处放一个罗盘.导线没有通电时罗盘的指针(小磁针的N极)指向北方;当给导线通入电流时,发现罗盘的指针偏转一定角度,根据偏转角度即可测定电流磁场的磁感应强度.现已测出此地的地磁场水平分量Be=5.0×10-5T,通电后罗盘指针停在北偏东60°的位置(如图所示).由此测出该通电直导线在其正下方10cm处产生磁场的磁感应强度大小为( )
(2012?石家庄一模)在实验精度要求不高的情况下,可利用罗盘来测量电流产生磁场的磁感应强度.具体做法是:在一根南北方向放置的直导线的正下方10cm处放一个罗盘.导线没有通电时罗盘的指针(小磁针的N极)指向北方;当给导线通入电流时,发现罗盘的指针偏转一定角度,根据偏转角度即可测定电流磁场的磁感应强度.现已测出此地的地磁场水平分量Be=5.0×10-5T,通电后罗盘指针停在北偏东60°的位置(如图所示).由此测出该通电直导线在其正下方10cm处产生磁场的磁感应强度大小为( ) (2012?石家庄一模)如图所示,足够长的传送带以恒定速率顺时针运行,将一个物体轻轻放在传送带底端,物体第一阶段被加速到与传送带具有相同的速度,第二阶段与传送带相对静止,匀速运动到达传送带顶端.下列说法正确的是( )
(2012?石家庄一模)如图所示,足够长的传送带以恒定速率顺时针运行,将一个物体轻轻放在传送带底端,物体第一阶段被加速到与传送带具有相同的速度,第二阶段与传送带相对静止,匀速运动到达传送带顶端.下列说法正确的是( ) (2012?石家庄一模)如图所示,a,b,c是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为20V,b点电势为24V,d点电势为12V,一个质子从b点以v0的速度射入此电场,入射方向与bc成45°角,一段时间后经过c点.不计质子的重力,下列判断正确的是( )
(2012?石家庄一模)如图所示,a,b,c是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为20V,b点电势为24V,d点电势为12V,一个质子从b点以v0的速度射入此电场,入射方向与bc成45°角,一段时间后经过c点.不计质子的重力,下列判断正确的是( )