题目内容
15.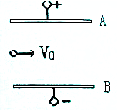 质量m=0.1kg,带电荷量q=-4×10-7C的带电微粒以v0=10m/s的速度从水平放置的平行金属板A、B的中央飞入板间,如图所示,已知板长L=1.0m,板间距离d=0.06m,问AB间所加电压在什么范围内带电粒子能从板间飞出?
质量m=0.1kg,带电荷量q=-4×10-7C的带电微粒以v0=10m/s的速度从水平放置的平行金属板A、B的中央飞入板间,如图所示,已知板长L=1.0m,板间距离d=0.06m,问AB间所加电压在什么范围内带电粒子能从板间飞出?
分析 当电场力大于重力时,向上偏转,根据牛顿第二定律与运动学公式可求出对应的电压;当电场力小于重力时,向下偏转,同理可求出对应的电压.从而确定电压的范围.
解答 解:当电压UAB比较大时,即qE>mg,粒子向上偏,$\frac{{U}_{1}q}{d}-mg=m{a}_{1}$
当刚好能从上板边缘飞出时,
有:$y=\frac{d}{2}=\frac{1}{2}{a}_{1}{t}^{2}$=$\frac{1}{2}{a}_{1}(\frac{L}{{v}_{0}})^{2}$,
即:$\frac{0.06}{2}=\frac{1}{2}{a}_{1}(\frac{1}{10})^{2}$,
解得:a1=6m/s2,
代入得:$\frac{{U}_{1}×4×1{0}^{-7}}{0.06}-0.1×10=0.1×6$
解得,U1=2.4×105V
当电压UAB比较小时,即qE<mg,粒子向下偏,
设刚好能从下板边缘飞出,
有:mg-$\frac{{U}_{2}q}{d}=m{a}_{2}$
y=$\frac{1}{2}$a2t2=$\frac{d}{2}$,即:$\frac{0.06}{2}=\frac{1}{2}{a}_{2}(\frac{1}{10})^{2}$,
解得:a2=6m/s2,代入得:$0.1×10-\frac{{U}_{2}×4×1{0}^{-7}}{0.06}=0.1×6$
解得:U2=6×104 V.
则要使粒子能从板间飞出,A、B间所加电压的范围为6×104 V≤UAB≤2.4×105V.
答:AB间所加电压在6×104 V≤UAB≤2.4×105V带电粒子能从板间飞出.
点评 本题考查重力与电场力大小的关系,何时做直线运动,何时做曲线运动,及如何处理类平抛运动方法.突出牛顿第二定律与运动学公式的重要性.

 名校课堂系列答案
名校课堂系列答案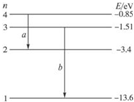
| A. | 由于放出光子,原子的能量增加 | |
| B. | 光子a的能量大于光子b的能量 | |
| C. | 光子a的波长大于光子b的波长 | |
| D. | 若光子a能使某金属发生光电效应,则光子b一定能使该金属发生光电效应 |

| A. | 电场强度比较是EA>EB | |
| B. | 电势比较是φA<φB | |
| C. | 电势差比较是UAB=UBC | |
| D. | 检验电荷沿AC方向移动电场力不做功 |
| A. | 它们的分子数不同,而分子的平均动能相同 | |
| B. | 它们的分子数相同,分子的平均动能也相同 | |
| C. | 分子的平均动能不同,冰小,水大 | |
| D. | 它们的内能不同,冰少,水多 |
| A. | 角速度与线速度成正比 | B. | 角速度与周期成反比 | ||
| C. | 线速度与周期成正比 | D. | 角速度与频率成反比 |
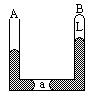 A端开口,B端封闭的粗细均匀的U型玻璃管,注入水银后有a、b两段空气被密封如图所示,设外界大气压不变,今使整个U型管的温度升高( )
A端开口,B端封闭的粗细均匀的U型玻璃管,注入水银后有a、b两段空气被密封如图所示,设外界大气压不变,今使整个U型管的温度升高( )| A. | A端水银上升,B端水银下降 | |
| B. | A、B两端水银面都上升,但水银面高度差变小 | |
| C. | A、B两端水银面都上升,但水银面高度差变大 | |
| D. | A、B两端水银面都上升,但水银面高度差不变 |

 如图所示,在一二象限内-R≤x≤R范围内有竖直向下的匀强电场E,电场的上边界方程为y=$\frac{1}{2R}$x2.在三四象限内存在垂直于纸面向里、边界方程为x2+y2=R2的匀强磁场.现在第二象限中电场的上边界有许多质量为m,电量为q的正离子,在y=$\frac{1}{2}$R处有一荧光屏,当正离子达到荧光屏时会发光,不计重力和离子间相互作用力.
如图所示,在一二象限内-R≤x≤R范围内有竖直向下的匀强电场E,电场的上边界方程为y=$\frac{1}{2R}$x2.在三四象限内存在垂直于纸面向里、边界方程为x2+y2=R2的匀强磁场.现在第二象限中电场的上边界有许多质量为m,电量为q的正离子,在y=$\frac{1}{2}$R处有一荧光屏,当正离子达到荧光屏时会发光,不计重力和离子间相互作用力.