题目内容
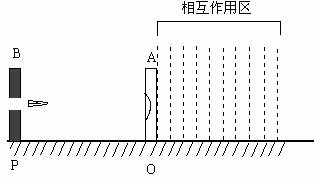
如图所示:质量 M = .040 kg的靶盒A位于光滑水平导轨上,开始时静止在O点,在O点右侧有范围很广的“相互作用区域”,如图中划虚线部分,当靶盒A进入相互作用区时便指向O点的恒力F= 20N作用,P处有一固定的发射器B,它可根据需要瞄准靶盒每次发射一颗水平速度 v 0 = 50m / s ,质量m = .010kg的子弹,当子弹打入靶盒A后,便留在盒内,碰撞时间极短。今约定,每当靶盒A 停在或到达O点时,都有一颗子弹进入靶盒A内。⑴ 当第一颗子弹进入靶盒A后,靶盒A离开O点最大距离为多少?
⑵ 当第三颗子弹进入靶盒A后,靶盒A从离开O点到又回到O点所经历时间为多少?
⑶ 求发射器B至少发射几颗子弹后,靶盒A在相互作用区内运动的距离不超过0.2m?
(1)设第一颗子弹进入靶盒A后,子弹与靶盒A共同速度为V1。根据碰撞过程系统动量守恒,有:mV0 = (m + M ) V12 (1)设A离开O点的最大距离为S1 ,根据动能定理有:-FS1 = 0 - (m + M) V1/2 (2 )由(1)、(2)式得S1 = 1.25 m (3)评分标准:(1)、(2)、(3)式各2分(2) 根据题意,A在恒力F作用下返回O点时第二颗子弹打入,由于A的动量与第二颗子弹动量大小相同、方向相反,第二颗子弹打入后A将静止在O点。设第三颗子弹打入A后,它们的共同速度为V3由系统动量守恒:mV0 = (M +3 m ) V3 (4)设A从离开O点到又回到O点经历时间为t ,且碰后A运动方向为正方向,由动量定理得:-Ft / 2 = 0 - (M +3 m ) V3 (5)由 (4)、(5) 两式得:t = 0.5 s (6)评分标准:必要文字叙述 1 分,(4)、(5)、(6)三式各2分(3) 设B 至少发射n颗子弹,且碰后A的速度为Vn 由系统动量守恒:mV0 = (M + n m ) Vn (7)由动能定理:-FSn = 0 - (M +nm ) Vn2 /2 (8)根据题意:Sn < 0.2 m (9)由 (7 ) 、(8 )、( 9 ) 式得:n >27 所以B至少发射28颗子弹 (10)评分标准:( 9 ) 式 1分,其余各式各2分

练习册系列答案
相关题目
 如图所示,质量m=0.1kg的导体棒静止于倾角为30度的斜面上,导体棒长度L=0.5m,通入垂直纸面向里的电流,电流大小I=2A,整个装置处于磁感应强度B=0.5T,方向竖直向上的匀强磁场中.求:
如图所示,质量m=0.1kg的导体棒静止于倾角为30度的斜面上,导体棒长度L=0.5m,通入垂直纸面向里的电流,电流大小I=2A,整个装置处于磁感应强度B=0.5T,方向竖直向上的匀强磁场中.求: 如图所示,质量M=50kg的空箱子,静止在光滑水平面上,箱子中有一个质量
如图所示,质量M=50kg的空箱子,静止在光滑水平面上,箱子中有一个质量 如图所示,质量m=5kg的物体,置于倾角θ=37°的足够长斜面上,用一平行于斜面的大小为30N的力推物体,物体沿斜面向上匀速运动.
如图所示,质量m=5kg的物体,置于倾角θ=37°的足够长斜面上,用一平行于斜面的大小为30N的力推物体,物体沿斜面向上匀速运动.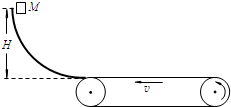 如图所示,质量M=20kg的物体从光滑曲面上高度H=0.8m处由静止释放,到达曲面底端时以水平方向的速度进入水平传送带.传送带由一电动机驱动,传送带的上表面匀速向左运动,运动速率为3.0m/s.已知物体与传送带间的动摩擦因数μ=0.10.(g取10m/s2)
如图所示,质量M=20kg的物体从光滑曲面上高度H=0.8m处由静止释放,到达曲面底端时以水平方向的速度进入水平传送带.传送带由一电动机驱动,传送带的上表面匀速向左运动,运动速率为3.0m/s.已知物体与传送带间的动摩擦因数μ=0.10.(g取10m/s2) 如图所示,质量M=0.3kg的长木板静止在光滑水平面上,质量m=0.2kg的小滑块静止在长木板的左端,滑块与长木板间滑动摩擦因数μ=0.3,在小滑块上作用一水平向右的恒力F,F的大小为1.5N,F作用2s后撤去,滑块始终没有滑离长木块.(g=10m/s2)
如图所示,质量M=0.3kg的长木板静止在光滑水平面上,质量m=0.2kg的小滑块静止在长木板的左端,滑块与长木板间滑动摩擦因数μ=0.3,在小滑块上作用一水平向右的恒力F,F的大小为1.5N,F作用2s后撤去,滑块始终没有滑离长木块.(g=10m/s2)