题目内容
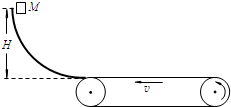 如图所示,质量M=20kg的物体从光滑曲面上高度H=0.8m处由静止释放,到达曲面底端时以水平方向的速度进入水平传送带.传送带由一电动机驱动,传送带的上表面匀速向左运动,运动速率为3.0m/s.已知物体与传送带间的动摩擦因数μ=0.10.(g取10m/s2)
如图所示,质量M=20kg的物体从光滑曲面上高度H=0.8m处由静止释放,到达曲面底端时以水平方向的速度进入水平传送带.传送带由一电动机驱动,传送带的上表面匀速向左运动,运动速率为3.0m/s.已知物体与传送带间的动摩擦因数μ=0.10.(g取10m/s2)(1)物体滑上传送带时的速度为多大?
(2)若两皮带轮之间的距离是6.0m,物体滑上传送带后立刻移走光滑曲面,物体将从哪一边离开传送带?通过计算说明你的结论.
(3)若皮带轮间的距离足够大,从M滑上到离开传送带的整个过程中,由于M和传送带间的摩擦而产生了多少热量?
分析:(1)滑块M从顶部滑到底端过程,机械能守恒,根据守恒定律列式求解即可;
(2)由牛顿第二定律可求得物体在传送带上运动时的加速度,则可求得物体的运动情况,进而确定小球从哪一端离开;
(3)摩擦力与物体和传送带之间的相对滑动位移的乘积转化为热量.
(2)由牛顿第二定律可求得物体在传送带上运动时的加速度,则可求得物体的运动情况,进而确定小球从哪一端离开;
(3)摩擦力与物体和传送带之间的相对滑动位移的乘积转化为热量.
解答:解:(1)物体沿曲面下滑的过程中机械能守恒,mgH=
m
解得物体滑到底端时的速度v0=
=μg=4.0 m/s
(2)以地面为参照系,物体滑上传送带后向右做匀减速运动直到速度为零,物体的加速度大小为:
a=
=μg=1.0m/s2
物体从滑上传送带到相对地面速度减小到零,向右的位移
S1=
=8.0 m>6.0 m,表明物体将从右边离开传送带.
(3)以地面为参考系,若两皮带轮间的距离足够大,则物体滑上传送带后向右做匀减速运动直到速度为零,后向左做匀加速运动,直到速度与传送带速度v相等后与传送带相对静止,从传送带左端掉下,其间物体的加速度大小和方向都不变,加速度大小
a=
=μg=1.0m/s2
取向右为正方向,从物体滑上传送带到与传送带相对静止的过程中,物体发生的位移
S1=
=3.5 m
物体运动的时间为
t=
=7.0 s
这段时间内皮带向左运动的位移S2=vt=21m
物体相对于传送带滑行的距离△S=S1+S2=24.5 m
物体与传送带相对滑动期间产生的热量
Q=Ff?△S=μMg?△S=490 J
答:(1)物体滑上传送带时的速度为4.0m/s;
(2)若两皮带轮之间的距离是6.0m,物体滑上传送带后立刻移走光滑曲面,物体将从右侧离开传送带;
(3)若皮带轮间的距离足够大,从M滑上到离开传送带的整个过程中,由于M和传送带间的摩擦而产生了490 J的热量.
| 1 |
| 2 |
| v | 2 0 |
解得物体滑到底端时的速度v0=
| Ff |
| M |
(2)以地面为参照系,物体滑上传送带后向右做匀减速运动直到速度为零,物体的加速度大小为:
a=
| Ff |
| M |
物体从滑上传送带到相对地面速度减小到零,向右的位移
S1=
0-
| ||
| -2a |
(3)以地面为参考系,若两皮带轮间的距离足够大,则物体滑上传送带后向右做匀减速运动直到速度为零,后向左做匀加速运动,直到速度与传送带速度v相等后与传送带相对静止,从传送带左端掉下,其间物体的加速度大小和方向都不变,加速度大小
a=
| Ff |
| M |
取向右为正方向,从物体滑上传送带到与传送带相对静止的过程中,物体发生的位移
S1=
0-
| ||
| -2a |
物体运动的时间为
t=
| v-v0 |
| -a |
这段时间内皮带向左运动的位移S2=vt=21m
物体相对于传送带滑行的距离△S=S1+S2=24.5 m
物体与传送带相对滑动期间产生的热量
Q=Ff?△S=μMg?△S=490 J
答:(1)物体滑上传送带时的速度为4.0m/s;
(2)若两皮带轮之间的距离是6.0m,物体滑上传送带后立刻移走光滑曲面,物体将从右侧离开传送带;
(3)若皮带轮间的距离足够大,从M滑上到离开传送带的整个过程中,由于M和传送带间的摩擦而产生了490 J的热量.
点评:要注意分析产生的热量即为摩擦力与相对位移间的乘积,再由能量守恒即可求得总能量,要注意分析能量间的相互转化.

练习册系列答案
相关题目
 (2013?荆州模拟)如图所示,质量m=2.2kg的金属块放在水平地板上,在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下,以速度v=5.0m/s向右做匀速直线运动.(cos37°=0.8,sin37°=0.6,取g=10m/s2)求:
(2013?荆州模拟)如图所示,质量m=2.2kg的金属块放在水平地板上,在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下,以速度v=5.0m/s向右做匀速直线运动.(cos37°=0.8,sin37°=0.6,取g=10m/s2)求: 如图所示,质量m=2.0kg的木块静止在水平面上,用大小F=20N、方向与水平方向成θ=37°角的力拉动木块,当木块运动到x=10m时撤去力F.不计空气阻力.已知木块与水平面间的动摩擦因数?=0.2,sin37°=0.6,cos37°=0.8.g取10m/s2.求:
如图所示,质量m=2.0kg的木块静止在水平面上,用大小F=20N、方向与水平方向成θ=37°角的力拉动木块,当木块运动到x=10m时撤去力F.不计空气阻力.已知木块与水平面间的动摩擦因数?=0.2,sin37°=0.6,cos37°=0.8.g取10m/s2.求: 如图所示,质量m=2.0×104kg的汽车以不变的速度先后驶过凹形桥面和凸形桥面,两桥面的圆弧半径均为20m.由于轮胎太旧,如果受到超过3×105N的压力时就会出现爆胎,则:
如图所示,质量m=2.0×104kg的汽车以不变的速度先后驶过凹形桥面和凸形桥面,两桥面的圆弧半径均为20m.由于轮胎太旧,如果受到超过3×105N的压力时就会出现爆胎,则: 如图所示,质量m=2.0kg的金属块放在水平地板上,在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下,以速度v=5.0m/s向右做匀速直线运动.(cos37°=0.8,sin37°=0.6,取g=10m/s2)求:
如图所示,质量m=2.0kg的金属块放在水平地板上,在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下,以速度v=5.0m/s向右做匀速直线运动.(cos37°=0.8,sin37°=0.6,取g=10m/s2)求: (2013?海淀区一模)如图所示,质量m=2.0×10-4kg、电荷量q=1.0×10-6C的带正电微粒静止在空间范围足够大的电场强度为E1的匀强电场中.取g=10m/s2.
(2013?海淀区一模)如图所示,质量m=2.0×10-4kg、电荷量q=1.0×10-6C的带正电微粒静止在空间范围足够大的电场强度为E1的匀强电场中.取g=10m/s2.