题目内容
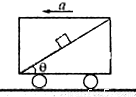
 如图所示,一物体放置在倾角为θ的斜面上,斜面固定于加速上升的电梯重,加速度为a,在物体始终相对于斜面静止的条件下,下列说法正确的是( )
如图所示,一物体放置在倾角为θ的斜面上,斜面固定于加速上升的电梯重,加速度为a,在物体始终相对于斜面静止的条件下,下列说法正确的是( )分析:以物体为研究对象进行受力分析,由牛顿第二定律可知物体受到的合力;再由力的合成与分解规律可得出斜面对物体的正压力及摩擦力.
解答:解:以物体为研究对象,分析其受力并建立直角坐标系,如图所示.
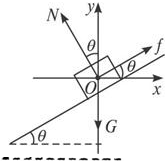
在y轴方向上由牛顿定律有:fsinθ+Ncosθ-mg=ma
在x轴方向上由受力平衡得:
Nsinθ=fcosθ ②
解①②式得N=m(g+a)cosθ,f=m(g+a)sinθ.
可见,当θ一定时,a越大,斜面对物体的正压力越大,斜面对物体的摩擦力越大;故AB错误;
当a一定时,θ越大,斜面对物体的正压力越小,斜面对物体的摩擦力越大,故选项C正确D错误;
故选C.

在y轴方向上由牛顿定律有:fsinθ+Ncosθ-mg=ma
在x轴方向上由受力平衡得:
Nsinθ=fcosθ ②
解①②式得N=m(g+a)cosθ,f=m(g+a)sinθ.
可见,当θ一定时,a越大,斜面对物体的正压力越大,斜面对物体的摩擦力越大;故AB错误;
当a一定时,θ越大,斜面对物体的正压力越小,斜面对物体的摩擦力越大,故选项C正确D错误;
故选C.
点评:本题注意物体的加速度方向为竖直向上,故合力一定沿竖直方向;故可以将力向水平方向和竖直方向进行分解.

练习册系列答案
相关题目
 如图所示,一物体放置在倾角为θ的斜面上,斜面固定于在水平面上加速运动的小车中,加速度为α,在物体始终相对于斜面静止的条件下,下列说法中正确的是( )
如图所示,一物体放置在倾角为θ的斜面上,斜面固定于在水平面上加速运动的小车中,加速度为α,在物体始终相对于斜面静止的条件下,下列说法中正确的是( )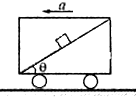 如图所示,一物体放置在倾角为θ的斜面上,斜面固定于在水平面上加速运动的小车中,加速度为α,在物体始终相对于斜面静止的条件下,下列说法中正确的是
如图所示,一物体放置在倾角为θ的斜面上,斜面固定于在水平面上加速运动的小车中,加速度为α,在物体始终相对于斜面静止的条件下,下列说法中正确的是