题目内容
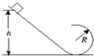 物体的质量为m,沿光滑的弯曲轨道滑下,轨道的形状如图所示,与弯曲轨道相接的圆轨道的半径为R,要使物体恰能通过圆轨道的最高点,物体应从离轨道最低处多高的地方由静止开始滑下?
物体的质量为m,沿光滑的弯曲轨道滑下,轨道的形状如图所示,与弯曲轨道相接的圆轨道的半径为R,要使物体恰能通过圆轨道的最高点,物体应从离轨道最低处多高的地方由静止开始滑下?分析:物体恰能通过圆轨道的最高点,重力提供向心力,根据牛顿第二定律列式;整个过程中只有重力做功,机械能守恒,根据守恒定律列方程;最后联立求解即可.
解答:解:方法一
物体恰能通过圆轨道的最高点,
有mg=m
重力势能的减少量:△Ep=mg(h-2R)
动能的增加量:△Ek=
mv2
根据机械能守恒,有△Ep=△Ek,
即 mg(h-2R)=
mv2
解得 h=
R.
答:物体应从离轨道最低处
R的地方由静止开始滑下.
方法二
物体恰能通过圆轨道的最高点,
有mg=m
只有重力做功:WG=mg(h-2R)
动能的改变量:△Ek=
mv2
根据动能定理:WG=△Ek
即 mg(h-2R)=
mv2
解得 h=
R.
答:物体应从离轨道最低处
R的地方由静止开始滑下.
物体恰能通过圆轨道的最高点,
有mg=m
| v2 |
| R |
重力势能的减少量:△Ep=mg(h-2R)
动能的增加量:△Ek=
| 1 |
| 2 |
根据机械能守恒,有△Ep=△Ek,
即 mg(h-2R)=
| 1 |
| 2 |
解得 h=
| 1 |
| 2 |
答:物体应从离轨道最低处
| 1 |
| 2 |
方法二
物体恰能通过圆轨道的最高点,
有mg=m
| v2 |
| R |
只有重力做功:WG=mg(h-2R)
动能的改变量:△Ek=
| 1 |
| 2 |
根据动能定理:WG=△Ek
即 mg(h-2R)=
| 1 |
| 2 |
解得 h=
| 1 |
| 2 |
答:物体应从离轨道最低处
| 1 |
| 2 |
点评:本题关键是明确小球的运动规律,然后根据牛顿第二定律和机械能守恒定律列方程联立求解;突破口在于小球恰好经过最高点时重力恰好提供向心力.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
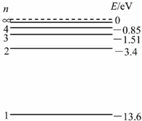 (1)氢原子的能级图如图所示,已知可见光光子的能量范围约为1.62eV-3.11eV,假定光子能量为E的一束光照射容器中大量处于n=2能级的氢原子,氢原子吸收光子后,发出频率为v1、v2、v3、v4、v5、和v6,且频率依次增大,关于这些光,下列说法中正确的是
(1)氢原子的能级图如图所示,已知可见光光子的能量范围约为1.62eV-3.11eV,假定光子能量为E的一束光照射容器中大量处于n=2能级的氢原子,氢原子吸收光子后,发出频率为v1、v2、v3、v4、v5、和v6,且频率依次增大,关于这些光,下列说法中正确的是
 (1)下列说法正确的是
(1)下列说法正确的是 与劲度系数为K的轻质弹簧连接,右端与劲度系数为2K的轻质弹簧连接,左右两弹簧原长均为L0,弹簧的另一端均固定在墙壁上.将物体拉离平衡位置,放手后,物体在光滑水平面上往复运动,证明物体的运动是简谐运动并求简谐运动的平衡位置.
与劲度系数为K的轻质弹簧连接,右端与劲度系数为2K的轻质弹簧连接,左右两弹簧原长均为L0,弹簧的另一端均固定在墙壁上.将物体拉离平衡位置,放手后,物体在光滑水平面上往复运动,证明物体的运动是简谐运动并求简谐运动的平衡位置.


 (1)如图所示,轻弹簧一端固定在墙上,另一端连一挡板,挡板的质量为m,一物体沿光滑水平面以一定的速度撞向挡板,物体质量为M,物体与挡板相接触的一面都装有尼龙搭扣,使得它们相撞后立即粘连在一起,若碰撞时间极短(即极短时间内完成粘连过程),则对物体M、挡板m和弹簧组成的系统,下面说法中正确的是:
(1)如图所示,轻弹簧一端固定在墙上,另一端连一挡板,挡板的质量为m,一物体沿光滑水平面以一定的速度撞向挡板,物体质量为M,物体与挡板相接触的一面都装有尼龙搭扣,使得它们相撞后立即粘连在一起,若碰撞时间极短(即极短时间内完成粘连过程),则对物体M、挡板m和弹簧组成的系统,下面说法中正确的是:
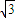 ,AB是一条直径,今有一束平行光沿AB方向射向圆柱体,试求:
,AB是一条直径,今有一束平行光沿AB方向射向圆柱体,试求:
