题目内容
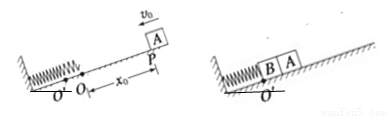
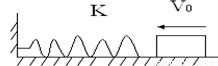
 (1)如图所示,轻弹簧一端固定在墙上,另一端连一挡板,挡板的质量为m,一物体沿光滑水平面以一定的速度撞向挡板,物体质量为M,物体与挡板相接触的一面都装有尼龙搭扣,使得它们相撞后立即粘连在一起,若碰撞时间极短(即极短时间内完成粘连过程),则对物体M、挡板m和弹簧组成的系统,下面说法中正确的是:
(1)如图所示,轻弹簧一端固定在墙上,另一端连一挡板,挡板的质量为m,一物体沿光滑水平面以一定的速度撞向挡板,物体质量为M,物体与挡板相接触的一面都装有尼龙搭扣,使得它们相撞后立即粘连在一起,若碰撞时间极短(即极短时间内完成粘连过程),则对物体M、挡板m和弹簧组成的系统,下面说法中正确的是:ACD
ACD
A.在M与m相撞的过程中,系统的动量守恒而机械能不守恒
B.在M与m相撞的过程中,系统的动量不守恒而机械能守恒
C.从M与m开始接触到弹簧被压缩到最短的过程中,系统的动量和机械能都不守恒
D.从M与m相撞后到弹簧第一次恢复原长的过程中,系统的动量不守恒而机械能守恒
(2)大量的氢原子处于n=2的激发态,当它们跃迁回基态时,将放出大量光子,用这些光予照射金属铯时.求:
(1)从铯表面飞出的电子的最大初动能是多少电了伏?(已知氢原子基态能量为-13.6eV,铯的逸出功为1.88eV)
(2)这些电子的截止电压是多少?
分析:(1)当系统所受的外力之和为零时,系统动量守恒;根据系统机械能守恒的条件判断系统机械能是否守恒.
(2)根据能级跃迁满足的规律求出释放的光子能量,结合光电效应方程求出光电子的最大初动能.
根据光电子的最大初动能,根据动能定理求出截止电压的大小.
(2)根据能级跃迁满足的规律求出释放的光子能量,结合光电效应方程求出光电子的最大初动能.
根据光电子的最大初动能,根据动能定理求出截止电压的大小.
解答:解:(1)A、在M与m相撞的过程中,有能量损失,所以系统机械能不守恒.碰撞的瞬间,由于时间极短,内力远大于外力,系统动量守恒.故A正确,B错误.
C、从M与m开始接触到弹簧被压缩到最短的过程中,墙壁对系统有作用力,即系统所受的外力之和不为零,系统动量不守恒,由于碰撞的过程有能量损失,系统机械能不守恒.故C正确.
D、从M与m相撞后到弹簧第一次恢复原长的过程中,由于墙壁对系统有外力作用,系统动量不守恒,对系统而言,只有弹簧的弹力做功,系统机械能守恒.故D正确.
故选:ACD.
(2)①氢原子处于n=2的激发态,当它们跃迁回基态时,放出的光子能量为hv=
×E1-E1=-
E1=-
×(-13.6)eV=10.2eV.
根据光电效应方程得,光电子的最大初动能Ekm=hv-W0=10.2-1.88eV=8.32eV.
②根据动能定理得,Ekm=eUc
知截止电压为UC=
=
=8.32V.
故答案为:(1)ACD;
(2)①从铯表面飞出的电子的最大初动能是8.32eV;
②截止电压8.32V.
C、从M与m开始接触到弹簧被压缩到最短的过程中,墙壁对系统有作用力,即系统所受的外力之和不为零,系统动量不守恒,由于碰撞的过程有能量损失,系统机械能不守恒.故C正确.
D、从M与m相撞后到弹簧第一次恢复原长的过程中,由于墙壁对系统有外力作用,系统动量不守恒,对系统而言,只有弹簧的弹力做功,系统机械能守恒.故D正确.
故选:ACD.
(2)①氢原子处于n=2的激发态,当它们跃迁回基态时,放出的光子能量为hv=
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
根据光电效应方程得,光电子的最大初动能Ekm=hv-W0=10.2-1.88eV=8.32eV.
②根据动能定理得,Ekm=eUc
知截止电压为UC=
| Ekm |
| e |
| 8.32eV |
| e |
故答案为:(1)ACD;
(2)①从铯表面飞出的电子的最大初动能是8.32eV;
②截止电压8.32V.
点评:解决本题的关键掌握机械能守恒和动量守恒的条件,以及掌握光电效应方程和能级跃迁所满足的规律.

练习册系列答案
相关题目
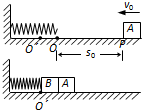 如图所示,轻弹簧左端固定在竖直墙上,右端点在O位置.质量为m的物块A(可视为质点)以初速度v0从距O点右方s0的P点处向左运动,与弹簧接触后压缩弹簧,将弹簧右端压到O?点位置后,A又被弹簧弹回.A离开弹簧后,恰好回到P点.物块A与水平面间的动摩擦因数为μ.求:
如图所示,轻弹簧左端固定在竖直墙上,右端点在O位置.质量为m的物块A(可视为质点)以初速度v0从距O点右方s0的P点处向左运动,与弹簧接触后压缩弹簧,将弹簧右端压到O?点位置后,A又被弹簧弹回.A离开弹簧后,恰好回到P点.物块A与水平面间的动摩擦因数为μ.求: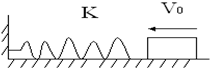 如图所示,轻质弹簧K一端与墙相连处于自然状态,质量为4kg木块沿光滑的水平面以5m/s的速度运动并开始挤压弹簧,求:
如图所示,轻质弹簧K一端与墙相连处于自然状态,质量为4kg木块沿光滑的水平面以5m/s的速度运动并开始挤压弹簧,求: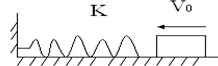
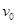 从距O点为
从距O点为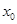 的P点沿斜面向下运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回。A离开弹簧后,恰好回到P点。物块A与斜面间的动摩擦因数为μ,斜面倾角为
的P点沿斜面向下运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回。A离开弹簧后,恰好回到P点。物块A与斜面间的动摩擦因数为μ,斜面倾角为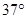 。求:
。求: