题目内容
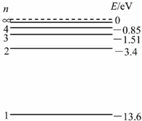 (1)氢原子的能级图如图所示,已知可见光光子的能量范围约为1.62eV-3.11eV,假定光子能量为E的一束光照射容器中大量处于n=2能级的氢原子,氢原子吸收光子后,发出频率为v1、v2、v3、v4、v5、和v6,且频率依次增大,关于这些光,下列说法中正确的是
(1)氢原子的能级图如图所示,已知可见光光子的能量范围约为1.62eV-3.11eV,假定光子能量为E的一束光照射容器中大量处于n=2能级的氢原子,氢原子吸收光子后,发出频率为v1、v2、v3、v4、v5、和v6,且频率依次增大,关于这些光,下列说法中正确的是A.氢原子发出b种频率光,有4种可能为可见光.
B.这束照射氢原子的光,它的光子能量E=hv6
C.用从n=2能级跃迁到n=1能级辐射出的光照射逸出功为6.34eV的金属铂能产生光电效应
D.频率最小的光v1具有显著的热效应
(2)在光滑的水平地面上静止着一质量为M=0.4kg的薄木板,一个质量为m=0.2kg的木块(可视为质点)以v0=4m/s的速度,从木板左端滑上,一段时间后,又从木板上滑下(不计木块滑下时机械能损失),两物体仍沿直线继续向前运动,从木块与木板刚刚分离开始计时,经时间t=3.0s,两物体之间的距离增加了s=3m,已知木块与木板的动摩擦因数μ=0.4,求薄木板的长度.

分析:(1)根据氢原子跃迁的频率条件和爱因斯坦的光电效应方程列式分析求解;
(2)木块和木板系统在水平方向不受外力,动量守恒,根据动量守恒定律和已知条件列式即可求出分离瞬间各自的速度;然后根据功能关系列式即可以求出木板的长度.
(2)木块和木板系统在水平方向不受外力,动量守恒,根据动量守恒定律和已知条件列式即可求出分离瞬间各自的速度;然后根据功能关系列式即可以求出木板的长度.
解答:解:(1)A、氢原子发出6种频率光,是从第4能及开始向低能级跃迁,共有6种跃迁方式,其中从第4、第3、第2能及向第一能及跃迁时,光电子的能量分别为:12.75eV、12.09eV、10.2eV,都不是可见光,故A错误;
B、这束照射氢原子的光,使氢原子从第二能级跃迁到第四能级,故其能量为:E=E4-E2=2.55eV,故B错误;
C、用从n=2能级跃迁到n=1能级辐射出的光能量为10.2eV,大于6.34eV的逸出功,故能发生光电效应,故C正确;
D、从第四能级跃迁到第三能级时,光子的能量最小,为1.51eV-0.85eV=0.66eV,小于红光光子的能量,为红外线,故D正确;
故选CD.
(2)设木块与木板分离后速度分别为为:v1、v2,由动量守恒定律得:
mv0=mv1+Mv2
根据题意,有
v1-v2=
解得:v1=2m/s,v2=1m/s
根据动能定理得:μmgd=
m
-
m
-
M
代入数据解得
d=1.25m
即薄木板的长度为1.25m.
B、这束照射氢原子的光,使氢原子从第二能级跃迁到第四能级,故其能量为:E=E4-E2=2.55eV,故B错误;
C、用从n=2能级跃迁到n=1能级辐射出的光能量为10.2eV,大于6.34eV的逸出功,故能发生光电效应,故C正确;
D、从第四能级跃迁到第三能级时,光子的能量最小,为1.51eV-0.85eV=0.66eV,小于红光光子的能量,为红外线,故D正确;
故选CD.
(2)设木块与木板分离后速度分别为为:v1、v2,由动量守恒定律得:
mv0=mv1+Mv2
根据题意,有
v1-v2=
| s |
| t |
解得:v1=2m/s,v2=1m/s
根据动能定理得:μmgd=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
代入数据解得
d=1.25m
即薄木板的长度为1.25m.
点评:本题第一问关键根据跃迁的频率条件和爱因斯坦的光电效应方程列式分析求解;第二问关键根据功能关系和动量守恒定律联立列式求解;

练习册系列答案
相关题目
 (1)氢原子的能级图如图所示,处于n=3激发态的大量氢原子向基态跃迁时所放出的光子中,只有一种光子不能使某金属A产生光电效应,则下列说法正确的是
(1)氢原子的能级图如图所示,处于n=3激发态的大量氢原子向基态跃迁时所放出的光子中,只有一种光子不能使某金属A产生光电效应,则下列说法正确的是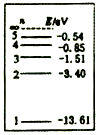
 .对于冰面的实验,请你与他们共同探讨以下二个问题:
.对于冰面的实验,请你与他们共同探讨以下二个问题:

