Question

【题目】如图所示，在xoy平面坐标系中，x轴上方存在电场强度E=1000v/m、方向沿y轴负方向的匀强电场；在x轴及与x轴平行的虚线PQ之间存在着磁感应强度为B=2T、方向垂直纸面向里的匀强磁场，磁场宽度为h．一个质量m=2×10-8kg、带电量q=+1.0×10-5C的粒子从y轴上（0，0.04）的位置以某一初度v0沿x轴正方向射入匀强电场，不计粒子的重力．

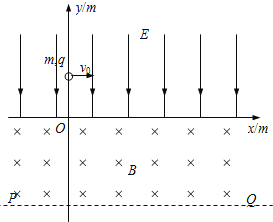
（1）若v0=200m/s，ⅰ求粒子第一次进入磁场时速度v的大小和方向；

（2）若磁场足够宽，求在磁场运动过程中粒子到x轴距离的最大值d.

（3）无论初速度v0大小如何，从该位置射入的所有粒子都能经磁场返回电场，求磁场宽度的最小值hm．

Answer 1

【答案】（1）200m/s，与x轴成45°角 （2）0.083m （3）0.2m

【解析】（1）ⅰ带电粒子垂直进入电场中做类平抛运动，根据牛顿第二定律得：Eq=ma

根据运动学公式有：y=at2

粒子刚进入磁场时竖直分速度大小为：vy=at=200m/s

根据几何关系有：v2=vx2+vy2

tanα=

代入数据解得：v=200m/s，与x轴成45°角

ⅱ.进入磁场后做匀速圆周运动．根据Bqv=m

运动过程中粒子到x轴的最大距离为d=r-rcosα

解得d=0.2(-1)≈0.083m

（2）Bqv=m

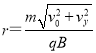
d＝rrcosθ＝＝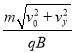

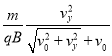
当v0=0时，运动过程中粒子到x轴的距离最大dm=0.2m要粒子经磁场返回电场，即不从磁场下边穿出，磁场的宽度h≥d，所以磁场宽度应为hmin=0.2m