题目内容
(18分)如图,一个质量为m的小球(可视为质点)以某一初速度从A点水平抛出,恰好从圆管BCD的B点沿切线方向进入圆弧,经BCD从圆管的最高点D射出,恰好又落到B点.已知圆弧的半径为R且A与D在同一水平线上,BC弧对应的圆心角θ=60°,不计空气阻力.求: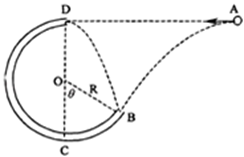
(1)小球从A点做平抛运动的初速度v0的大小;
(2)在D点处管壁对小球的作用力N;
(3)小球在圆管中运动时克服阻力做的功Wf.
(1)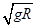 (2)N=
(2)N=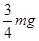 方向竖直向上 (3)
方向竖直向上 (3)
解析试题分析:(1)小球从A到B:竖直方向vy2=2gR(1+cos60°)
则vy==
在B点,由速度关系v0=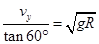
(2)小球从D到B:竖直方向R(1+cos60°)=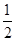 gt2
gt2
解得:t=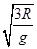
则小球从D点抛出的速度vD=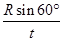 =
= 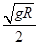 在D点,由向心力公式得:mg﹣N=
在D点,由向心力公式得:mg﹣N= 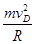
解得:N=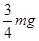 方向竖直向上
方向竖直向上
(3)从A到D全过程应用动能定理: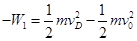 ,解得
,解得 
考点:本题考查了圆周运动、平抛运动和动能定理。

练习册系列答案
相关题目
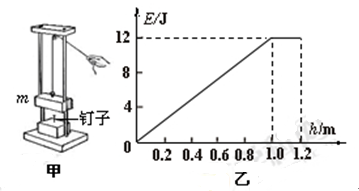
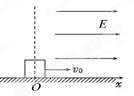
 kg,台高h=5.0m,摩托车的落地点到高台的水平距离x=10.0m。不计空气阻力,取
kg,台高h=5.0m,摩托车的落地点到高台的水平距离x=10.0m。不计空气阻力,取 。求:
。求:
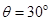 ,另一边与地面垂直,高为
,另一边与地面垂直,高为 ,斜面顶点有一定滑轮,物块A和B的质量分别为
,斜面顶点有一定滑轮,物块A和B的质量分别为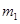 和
和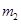 ,通过轻而软的细绳连结并跨过定滑轮,开始时两物块都位于与地面的垂直距离为
,通过轻而软的细绳连结并跨过定滑轮,开始时两物块都位于与地面的垂直距离为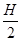 的位置上,释放两物块后,A沿斜面无摩擦地上滑,B沿斜面的竖直边下落,若物块A恰好能达到斜面的顶点,试求
的位置上,释放两物块后,A沿斜面无摩擦地上滑,B沿斜面的竖直边下落,若物块A恰好能达到斜面的顶点,试求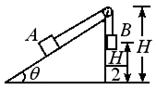
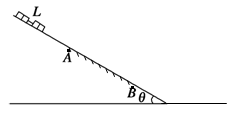
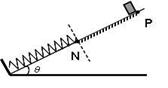
 的均匀粗钢丝绳固定在等高的
的均匀粗钢丝绳固定在等高的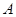 、
、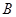 处,钢丝绳最低点与固定点
处,钢丝绳最低点与固定点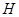 ,动滑轮起点在
,动滑轮起点在 的人抓住滑轮下方的挂钩由
的人抓住滑轮下方的挂钩由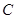 点,
点,
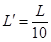 ,高度差为
,高度差为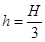 .若参赛者在运动过程中始终处于竖直状态,抓住滑轮的手与脚底之间的距离也为
.若参赛者在运动过程中始终处于竖直状态,抓住滑轮的手与脚底之间的距离也为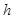 ,滑轮与钢丝绳间的摩擦力大小视为不变,且摩擦力所做功与滑过的路程成正比,不计参赛者在运动中受到的空气阻力、滑轮(含挂钩)的质量和大小,不考虑钢索桥的摆动及形变.
,滑轮与钢丝绳间的摩擦力大小视为不变,且摩擦力所做功与滑过的路程成正比,不计参赛者在运动中受到的空气阻力、滑轮(含挂钩)的质量和大小,不考虑钢索桥的摆动及形变.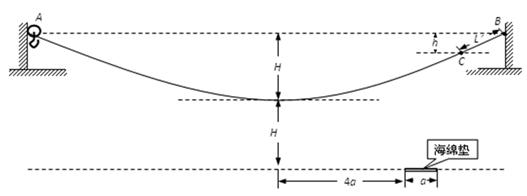
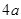 、宽度为
、宽度为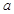 ,厚度不计的海绵垫子上.若参赛者由
,厚度不计的海绵垫子上.若参赛者由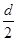 的N点时速度恰好为零.(重力加速度为g)
的N点时速度恰好为零.(重力加速度为g)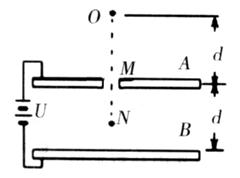
 的距离.质点仍从O点由静止自由下落,求质点下落速度为零时距B板的距离.
的距离.质点仍从O点由静止自由下落,求质点下落速度为零时距B板的距离.