Question

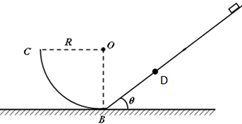如图所示，有一倾角θ=37°的足够长粗糙斜面，底端与一个光滑的

1

4

圆弧平滑连接，圆弧底端切线水平．一个质量为m=1kg的滑块（可视为质点）从斜面上某点A（图中未画出）由静止开始滑下，经过斜面底端B点后恰好到达圆弧最高点C，又从圆弧滑回，恰好能上升到斜面上的D点，再由D点沿斜面下滑至B点后沿圆弧上升，再滑回，这样往复运动，最后停在B点．已知圆弧半径R=0.8m，滑块与斜面间的动摩擦因数为μ=0.5，g=10m/s²，sin37°=0.6，cos37°=0.8，假设滑块经过斜面与圆弧平滑连接处速率不变．求：
（1）滑块第1次经过B点时的速度大小及对圆弧轨道的压力；
（2）图中BD两点的距离；
（3）滑块从开始运动到第5次经过B点的过程中与斜面摩擦而产生的热量．

Answer 1

分析：（1）根据动能定理求出质点第一次到达B点的速度，结合牛顿第二定律和第三定律求出质点对圆弧轨道的压力．
（2）对AB段和BD段分别运用动能定理，求出BD的长度．
（3）分别对上滑过程和下滑过程运用动能定理，得出上滑的位移与下滑的位移的关系，从而找出规律，得出质点在斜面上运动的路程，通过Q=fs求出产生的热量．

解答：解：（1）滑块从B到C的过程，机械能守恒mgR=

1

2

m

v

2 B

代入数据可得v_B=4m/s
所以在B点，对滑块有N-mg=m

v 2 B

R

代入数据得N=30N   
根据牛顿第三定律可得：滑块对圆弧轨道的压力为30N，方向竖直向下．
（2）滑块由B到D，据动能定理得-mglBDsinθ-μmgcosθlBD=0-

1

2

m

v

2 B

代入数据计算可得：l_BD=0.8m
（3）滑块由A到B，据动能定理mglADsinθ-μmgcosθlAD=

1

2

m

v

2 B

-0
代入数据计算可得l_AD=4m
滑块由D到B，动能定理：mgl_DBsinθ-μmgcosθl_BD=

1

2

mv²-0①
设滑块经B后滑上圆弧，又滑回，再次经B后滑上斜面的最高点为E，则滑块由B到E，据动能定理得-mgl_BEsinθ-μmgcosθ_BE=0-

1

2

mv²②
由①②可得l_BE=0.16m
所以，从开始到第五次经过B点产生的总热量为：Q=μmgcosθ（l_AD+2l_BD+2l_BE）=23.68J
答：（1）滑块第1次经过B点时的速度大小及对圆弧轨道的压力30N；
（2）图中BD两点的距离0.8m；
（3）滑块从开始运动到第5次经过B点的过程中与斜面摩擦而产生的热量23.68J．

点评：本题考查了考查了动能定理和牛顿第二定律，综合性较强，难度中等，关键是理清运动过程，选择合适的过程运用动能定理进行求解．