题目内容
 (2005?和平区一模)如图所示,有一倾角为30°的光滑斜面,斜面长l为10m,一小球从斜面顶端以10m/s的速度沿水平方向抛出,求:
(2005?和平区一模)如图所示,有一倾角为30°的光滑斜面,斜面长l为10m,一小球从斜面顶端以10m/s的速度沿水平方向抛出,求:(1)小球沿斜面滑到底端的时间t和水平位移S;
(2)小球到达斜面底端时的速度大小.(g取10m/s2).
分析:(1)小球的运动可以分解为沿初速度方向的匀速直线运动与垂直于初速度方向的初速度为零的匀加速运动,应用匀速运动与匀变速运动的运动规律可以求出小球的运动时间与水平位移.
(2)由动能定理可以求出小球到达斜面底端的速度.
(2)由动能定理可以求出小球到达斜面底端的速度.
解答:解:(1)在斜面上小球沿v0方向做匀速运动,
垂直v0方向做初速度为零的匀加速运动.
由牛顿第二定律得:ma=mgsin30°,
小球的加速度a=gsin30°=5m/s2,
沿v0方向位移s=v0t,
垂直v0方向:l=
at2,
解得,运动时间:t=
=
s=2s,
水平位移:s=v0
=10
m=20m;
(2)设小球运动到斜面底端时的速度为v,
由动能定理得:mglsin300=
mv2-
m
,
小球到达斜面底端时的速度v=
=
m/s=14.1m/s.
答:(1)小球沿斜面滑到底端的时间为2s,水平位移为20m.
(2)小球到达斜面底端时的速度大小为14.1m/s.
垂直v0方向做初速度为零的匀加速运动.
由牛顿第二定律得:ma=mgsin30°,
小球的加速度a=gsin30°=5m/s2,
沿v0方向位移s=v0t,
垂直v0方向:l=
| 1 |
| 2 |
解得,运动时间:t=
|
|
水平位移:s=v0
|
|
(2)设小球运动到斜面底端时的速度为v,
由动能定理得:mglsin300=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
小球到达斜面底端时的速度v=
|
| 102+10×10 |
答:(1)小球沿斜面滑到底端的时间为2s,水平位移为20m.
(2)小球到达斜面底端时的速度大小为14.1m/s.
点评:把小球在斜面上的运动分解为初速度方向的匀速运动与垂直于初速度方向的初速度为零的晕加速度运动,应用运动的合成与分解是正确解题的前提与关键.

练习册系列答案
相关题目

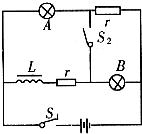 (2005?和平区一模)如图所示的电路中,A、B两灯电阻均为R,且R>r,L为纯电感线圈,原先S1,S2均断开,则( )
(2005?和平区一模)如图所示的电路中,A、B两灯电阻均为R,且R>r,L为纯电感线圈,原先S1,S2均断开,则( )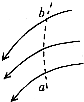 (2005?和平区一模)如图所示,实线为某电场局部的三条电场线,虚线为一个带负电的粒子仅在电场力作用下的运动轨迹,下列说法中正确的是( )
(2005?和平区一模)如图所示,实线为某电场局部的三条电场线,虚线为一个带负电的粒子仅在电场力作用下的运动轨迹,下列说法中正确的是( ) (2005?和平区一模)如图所示,甲图中线圈A的a,b两端加上如图乙所示的电压时,在时间0~t0内,线圈B中感应电流的方向及线圈B的受力方向是( )
(2005?和平区一模)如图所示,甲图中线圈A的a,b两端加上如图乙所示的电压时,在时间0~t0内,线圈B中感应电流的方向及线圈B的受力方向是( )