题目内容
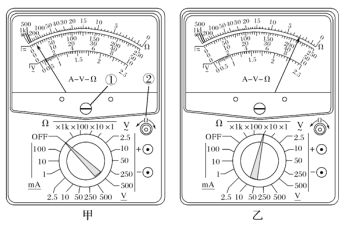
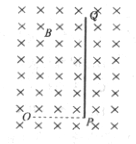
【题目】如图所示，有一个磁感应强度大小为B、方向垂直纸面向里的足够大的匀强磁场，在磁场中的O点有一个粒子源，能在纸面内向各个方向连续不断地均匀发射速率为v、比荷为k的带正电粒子，PQ是垂直纸面放置、厚度不计的挡板，挡板的P端与O点的连线与挡板垂直．带电粒子的重力以及粒子间的相互作用力忽略不计．
（1）为了使带电粒子不打在挡板上，粒子源到挡板的距离d应满足什么条件？
（2）若粒子源到挡板的距离
，且己知沿某一方向射出的粒子恰好经过挡板的P点后最终又打在挡板上，求这个粒子从O点射出时的速度方向；
（3）若粒子源到挡板的距离
，粒子打到挡板左、右表面上的长度之比是多少？
【答案】（1）
（2）30°（3）
【解析】（1）设带电粒子的质量为m，电荷量为q，在磁场中运动的轨道半径为r，
则由洛伦兹力充当向心力得： 
①
由题意得
②
由题意分析可知，为了使带电粒子不打在挡板上，d应满足：d>2r ③
由①②③解得
（2）如图所示，设粒子速度方向与OP连线的夹角为θ时，粒子恰好经过挡板的P点后最终又打在挡板右表面的N点．由图形的几何关系可知：△OPN为直角三角形，ON为粒子圆周运动的直径
由于
和①②可得
⑤
由几何关系可得θ＝30° ⑥
（3）粒子打到挡板左、右表面的示意图如图所示．由图可知，粒子打到挡板左表面的长度为
粒子打到挡板右表面的长度为
粒子打到挡板左、右表面上的长度之比为
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
