题目内容
3.做匀变速直线运动的物体的位移与时间的关系式为x=0.5t+t2,则经过多长时间它的速度为3m/s.( )| A. | 2.5s | B. | 1.25s | C. | 3s | D. | 2.4s |
分析 根据匀变速直线运动的位移时间公式得出物体的初速度和加速度,结合速度时间公式求出速度达到3m/s所需的时间.
解答 解:根据匀变速直线运动的位移时间公式得,x=${v}_{0}t+\frac{1}{2}a{t}^{2}=0.5t+{t}^{2}$,解得物体的初速度v0=0.5m/s,加速度a=2m/s2,
则速度达到3m/s所需的时间t=$\frac{v-{v}_{0}}{a}=\frac{3-0.5}{2}s=1.25s$.
故选:B.
点评 解决本题的关键掌握匀变速直线运动的位移时间公式、速度时间公式,并能灵活运用,基础题.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
13.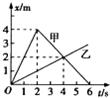 如图所示是甲乙两物体从同一点出发的位移-时间(x-t)图象,由图象可以看出在0〜4s这段时间内( )
如图所示是甲乙两物体从同一点出发的位移-时间(x-t)图象,由图象可以看出在0〜4s这段时间内( )
 如图所示是甲乙两物体从同一点出发的位移-时间(x-t)图象,由图象可以看出在0〜4s这段时间内( )
如图所示是甲乙两物体从同一点出发的位移-时间(x-t)图象,由图象可以看出在0〜4s这段时间内( )| A. | 甲、乙两物体始终同向运动 | B. | 4s时甲、乙两物体之间的距离最大 | ||
| C. | 甲的平均速度等于乙的平均速度 | D. | 甲、乙两物体之间的最大距离为4m |
11. 如图所示,重为12N的物块G1在三根细绳的悬挂下处于 静止状态,细绳BP在水平方向,细绳AP偏离竖直方向37°角,且连在重为50N的物块G2上,物块G2静止与倾角为37°的斜面上,取g=10m/s2.则下列说法正确的是( )
如图所示,重为12N的物块G1在三根细绳的悬挂下处于 静止状态,细绳BP在水平方向,细绳AP偏离竖直方向37°角,且连在重为50N的物块G2上,物块G2静止与倾角为37°的斜面上,取g=10m/s2.则下列说法正确的是( )
 如图所示,重为12N的物块G1在三根细绳的悬挂下处于 静止状态,细绳BP在水平方向,细绳AP偏离竖直方向37°角,且连在重为50N的物块G2上,物块G2静止与倾角为37°的斜面上,取g=10m/s2.则下列说法正确的是( )
如图所示,重为12N的物块G1在三根细绳的悬挂下处于 静止状态,细绳BP在水平方向,细绳AP偏离竖直方向37°角,且连在重为50N的物块G2上,物块G2静止与倾角为37°的斜面上,取g=10m/s2.则下列说法正确的是( )| A. | 绳BP对物块G2的拉力9N | B. | 绳PA对P点的拉力为20N | ||
| C. | 斜面对物块G2的支持力40N | D. | 斜面对物块G2的摩擦力为37.2N |
13.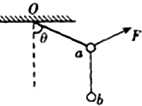 如图所示,将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a使整个装置处于平衡状态,且悬线Oa与竖直方向的夹角为θ=60°,则力F的大小可能为 ( )
如图所示,将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a使整个装置处于平衡状态,且悬线Oa与竖直方向的夹角为θ=60°,则力F的大小可能为 ( )
 如图所示,将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a使整个装置处于平衡状态,且悬线Oa与竖直方向的夹角为θ=60°,则力F的大小可能为 ( )
如图所示,将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a使整个装置处于平衡状态,且悬线Oa与竖直方向的夹角为θ=60°,则力F的大小可能为 ( )| A. | $\sqrt{3}$mg | B. | mg | C. | $\frac{\sqrt{3}}{2}$mg | D. | $\frac{\sqrt{3}}{3}$Lmg |