题目内容
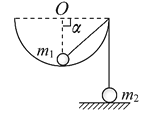
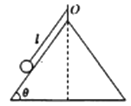
【题目】如图所示,底角为![]() 的圆锥体静止不动,顶端通过一根长为l=1.25m的细线悬挂一个质量为m=1kg的小球,细线处于张紧状态,若小球在水平面内做匀速圆周运动的角速度为ω=4rads时,不计一切阻力,g=10m/s2,则小球的向心加速度为
的圆锥体静止不动,顶端通过一根长为l=1.25m的细线悬挂一个质量为m=1kg的小球,细线处于张紧状态,若小球在水平面内做匀速圆周运动的角速度为ω=4rads时,不计一切阻力,g=10m/s2,则小球的向心加速度为
A. 10![]() m/s2 B. 10
m/s2 B. 10![]() m/s2 C. 15m/s2 D. 20m/s2
m/s2 C. 15m/s2 D. 20m/s2
【答案】B
【解析】
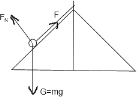
当小球对圆锥体刚好无压力时,向心力F=mgcotθ=mω2LCOSθ,
解得:![]() <ω=4rads
<ω=4rads
所以当ω=4rads时,小球离开斜面,设绳子与竖直方向的夹角为α,则
mgtanα=mω2lsinα,代入数据得cosα=0.5
小球的向心加速度:a=ω2lsinα=10![]() m/s2,故B正确,ACD错误。
m/s2,故B正确,ACD错误。
故选:B

练习册系列答案
相关题目