题目内容
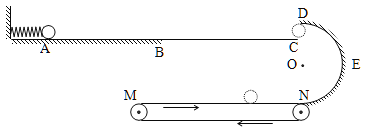
【题目】如图所示,是一传送装置,其中AB段粗糙,AB段长为L="1" m, 动摩擦因数μ=0.5;BC、DEN段均可视为光滑,DEN是半径为r=0.5 m的半圆形轨道,其直径DN沿竖直方向,C位于DN竖直线上,CD间的距离恰能让小球自由通过。其中N点又与足够长的水平传送带的右端平滑对接,传送带以6m/s的速率沿顺时针方向匀速转动,小球与传送带之间的动摩擦因数也为0.5。左端竖直墙上固定有一轻质弹簧,现用一可视为质点的小球压缩弹簧至A点后由静止释放(小球和弹簧不粘连),小球刚好能沿圆弧DEN轨道滑下,而始终不脱离轨道。已知小球质量m=0.2 kg ,g 取10m/s2。
(1)求小球到达D点时速度的大小及弹簧压缩至A点时所具有的弹性势能;
(2)小球第一次滑上传送带后的减速过程中,在传送带上留下多长的痕迹?
(3)如果希望小球能沿着半圆形轨道上下不断地来回运动,且始终不脱离轨道,则传送带的速度应满足什么要求?
【答案】(1)1.5J(2)8.5m(3)![]()
【解析】试题分析:(1)“小球刚好能沿DEN轨道滑下”,在圆周最高点D点必有:
![]()
得:vD=![]() m/s,
m/s,
从A点到D点,由能量守恒得:Ep=μmgL+![]() mvD2
mvD2
联立以上两式并代入数据得:Ep=1.5J
(2)从D到N,根据机械能守恒可得![]()
在传送带上物块![]()
![]()
物块向左减速![]()
![]()
物块向左运动的位移![]()
![]()
传送带向右运动的位移为![]()
![]()
留下的痕迹为![]()
(3)设物块在传送带上返回到右端的速度为v0,若物块恰能冲到EF轨道圆心的等高处,则
![]()
![]()
则传送带的速度必须满足![]()

练习册系列答案
相关题目