Question

【题目】在“验证牛顿运动定律”的实验中，采用如图所示的实验装置，小车及车中砝码的质量用M表示，所挂钩码的质量用m表示，小车的加速度可由小车后拖动的纸带打上的点计算出．

（1）当M与m的大小关系满足__________时，才可以认为绳对小车的拉力大小等于所挂钩码的重力．

（2）一组同学在做加速度与质量的关系实验时，保持所挂钩码的质量一定，改变小车及车中砝码的质量，测出相应的加速度，采用图象法处理数据．为了比较容易地检测出加速度a与质量M的关系，应该做a与_________的图象．

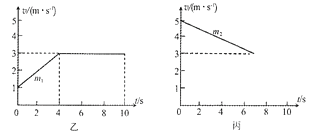
（3）如图乙，该同学根据测量数据做出的a-F图线，图象没过坐标原点的原因_______．

（4）如图乙，该同学根据测量数据做出的a-F图线，图象变弯曲的原因_________．

Answer 1

【答案】 M>>m 没有平衡摩擦力或者平衡摩擦力不足 不满足M>>m

【解析】试题分析：要求在什么情况下才可以认为绳对小车的拉力大小等于钩码的重力，需求出绳子的拉力，而要求绳子的拉力，应先以整体为研究对象求出整体的加速度，再以M为研究对象求出绳子的拉力，通过比较绳对小车的拉力大小和盘和盘中砝码的重力的大小关系得出只有m＜＜M时才可以认为绳对小车的拉力大小等于钩码的重力．反比例函数图象是曲线，而根据曲线很难判定出自变量和因变量之间的关系；正比例函数图象是过坐标原点的一条直线，就比较容易判定自变量和因变量之间的关系．图象表明当F≠0时，a=0．也就是说当绳子上有拉力时小车的加速度还为0，是没有平衡摩擦力，或平衡摩擦力不足引起的．
当小车的质量远大于钩码的总质量时，才能近似认为细线对小车的拉力大小等于钩码的总重力大小，否则图象将会发生弯曲．

（1）以整体为研究对象有，解得，以M为研究对象有绳子的拉力，显然要有F=mg必有m+M=M，故有，即只有时才可以认为绳对小车的拉力大小等于盘和盘中砝码的重力．

（2）根据牛顿第二定律F=Ma，a与M成反比，而反比例函数图象是曲线，而根据曲线很难判定出自变量和因变量之间的关系，故不能作a-M图象；但，故a与成正比，而正比例函数图象是过坐标原点的一条直线，就比较容易判定自变量和因变量之间的关系，故应作a-图象；

（3）小车质量M一定时，其加速度a与合力F成正比，图象应该为一条经过坐标原点的直线；由于实验中用勾码的重力代替小车的合力，故不可避免的会出现系统误差，乙图中，由于小车受到摩擦阻力，其合力小于绳子的拉力，所以不经过坐标原点；

（4）钩码加速下降，处于失重状态，拉力小于重力，要使勾码重力接进小车所受的拉力，只有让小车质量远大于勾码质量，否则，会出现乙图中的弯曲情况；