题目内容
我国的“嫦娥二号”卫星在贴近月球表面的圆轨道上运行的周期为l18分钟,又知道月球表面的重力加速度是地球表面重力加速度的
,万有引力常量为G,地球表面重力加速度为g,仅利用以上数据可以计算出( )
| 1 |
| 6 |
分析:第一宇宙速度是近表面运行的速度.根据万有引力等于重力得GM=gR2
解答:解:A、“嫦娥二号”卫星在贴近月球表面的圆轨道上运行的周期为l18分钟,月球表面的重力加速度是地球表面重力加速度的
,地球表面重力加速度为g,所以月球表面重力加速度为:g′=
g,
根据重力提供向心力得贴近月球表面的圆轨道上:a=
g=
所以可以求出月球半径R.第一宇宙速度是近表面运行的速度:v=
根据万有引力等于重力得:GM=g′R2
所以月球第一宇宙速度:v=
=
,故A正确
B、由于不知道“嫦娥二号”质量,所以不知道月球对“嫦娥二号”的引力,故B错误
C、根据万有引力等于重力得GM=g′R2
M=
,
根据密度ρ=
可以求出密度,故C正确
D、根据题意无法求出“嫦娥二号”的质量,故D错误
故选AC.
| 1 |
| 6 |
| 1 |
| 6 |
根据重力提供向心力得贴近月球表面的圆轨道上:a=
| 1 |
| 6 |
| 4π2R |
| T2 |
所以可以求出月球半径R.第一宇宙速度是近表面运行的速度:v=
|
根据万有引力等于重力得:GM=g′R2
所以月球第一宇宙速度:v=
|
| gR |
| g′R |
B、由于不知道“嫦娥二号”质量,所以不知道月球对“嫦娥二号”的引力,故B错误
C、根据万有引力等于重力得GM=g′R2
M=
| gR2 |
| G |
| g′R2 |
| G |
根据密度ρ=
| M |
| V |
D、根据题意无法求出“嫦娥二号”的质量,故D错误
故选AC.
点评:对卫星类型问题,要建立物理模型,心中有卫星运动的图景,再分析向心力的来源,由牛顿第二定律列方程求解有关物理量.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
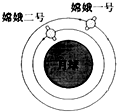 据报道,我国自主研制的“嫦娥二号”卫星在其环月飞行的高度距离月球表面100km时开始全面工作.“嫦娥二号”所探测到得有关月球的数据比环月飞行高度约为200km的“嫦娥一号”更加翔实.若两颗卫星环月运行均可视为匀速运动,运行轨道如图所示,则( )
据报道,我国自主研制的“嫦娥二号”卫星在其环月飞行的高度距离月球表面100km时开始全面工作.“嫦娥二号”所探测到得有关月球的数据比环月飞行高度约为200km的“嫦娥一号”更加翔实.若两颗卫星环月运行均可视为匀速运动,运行轨道如图所示,则( )| A、“嫦娥二号”环月运行的周期比“嫦娥一号”长 | B、“嫦娥二号”环月运行的速度比“嫦娥一号”大 | C、“嫦娥二号”环月运行时向心加速度比“嫦娥一号”大 | D、“嫦娥二号”环月运行时角速度比“嫦娥一号”小 |
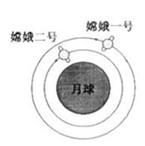
 ,万有引力常量为G,地球表面重力加速度为g,仅利用以上数据可以计算出( )
,万有引力常量为G,地球表面重力加速度为g,仅利用以上数据可以计算出( )