题目内容
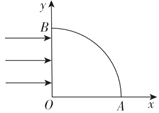
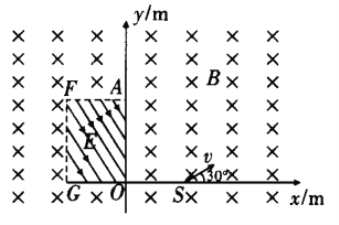
【题目】如图所示,在真空中建立一个平面直角坐标系xOy,y轴左边有一个矩形AOGF,F点坐标(-1m,![]() m),矩形区域内有与x轴正方向成
m),矩形区域内有与x轴正方向成![]() 角斜向下的匀强电场;矩形区域外有方向垂直于坐标轴平面向里,磁感应强度大小B=1.0T的足够大匀强磁场,在x轴上坐标(1m,0)处有一粒子发射源S,沿着与x轴正方向
角斜向下的匀强电场;矩形区域外有方向垂直于坐标轴平面向里,磁感应强度大小B=1.0T的足够大匀强磁场,在x轴上坐标(1m,0)处有一粒子发射源S,沿着与x轴正方向![]() 角斜向上发射带正电粒子,当发射速度v=1.5×106 m/s时,带电粒子恰好从区域的A点垂直电场方向进人匀强电场,并从坐标原点O离开电场,不计粒子的重力。求:
角斜向上发射带正电粒子,当发射速度v=1.5×106 m/s时,带电粒子恰好从区域的A点垂直电场方向进人匀强电场,并从坐标原点O离开电场,不计粒子的重力。求:
(1)带电粒子的比荷;
(2)电场强度E的大小;
(3)若要使带电粒子不进人电场区域,求发射速度(发射方向不变)的范围。
【答案】(1)1.5×106 C/kg(2)6×106N/C(3)v≥>3×106m/s 或v≤1×106m/s
【解析】
(1)A、S连线恰为直径才满足条件
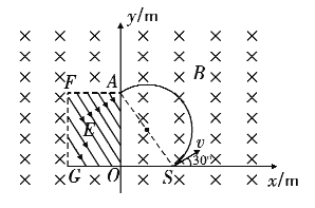
由图可知:R=lm
qvB=![]()
所以:
![]() ×106 C/kg
×106 C/kg
(2)在电场中做类平拋运动
vt=AOsin![]()
![]() =AOcos
=AOcos![]()
解得:
E=6×106N/C
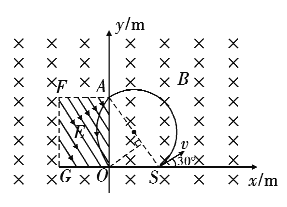
(3)半径很大,包围电场区边,圆心在A点:

R1=2m
qv1B=![]()
解得:
v1=3×106m/s
速度很小,半径小达不到电场区:
R2+R2cos60°=OS
解得:
R2=![]() m
m
qv2B=![]()
解得:
v2=1×106m/s
综合所得:速度v≥>3×106m/s 或v≤1×106m/s,电荷不会进入电场。

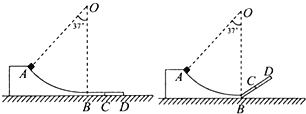
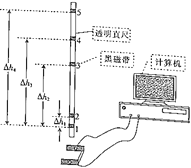
【题目】验证机械能守恒定律的方法很多,落体法验证机械能守恒定律就是其中的一种,图示是利用透明直尺自由下落和光电计时器来验证机械能守恒定律的简易示意图.当有不透光的物体从光电门间通过时,光电计时器就可以显示物体的挡光时间,所用的光电门传感器可测得最短时间为0.01ms.将挡光效果好、宽度d=3.8×10﹣3m的黑色磁带贴在透明直尺上,现将直尺从一定高度由静止释放,并使其竖直通过光电门.一同学测得各段黑色磁带通过光电门的时间△ti与图中所示的高度差△hi,并将部分数据进行了处理,结果如图所示.(取g=9.8m/s2,表格中M=0.1kg为直尺的质量)
△ti(×10﹣3s) | vi= | △Eki= | △hi(m) | Mghi(J) | |
1 | 1.21 | 3.14 | ﹣ | ﹣ | ﹣ |
2 | 1.15 | 3.30 | 0.052 | 0.06 | 0.059 |
3 | 1.00 | 3.80 | 0.229 | 0.24 | 0.235 |
4 | 0.95 | 4.00 | 0.307 | 0.32 | 0.314 | 5 | 0.90 | ① | ② | 0.41 | ③ |
(1)从表格中的数据可知,直尺上磁带通过光电门的瞬时速度是利用vi=![]() 求出的,请你简要分析该同学这样做的理由是:_____.
求出的,请你简要分析该同学这样做的理由是:_____.
(2)表格中的数据①、②、③分别为_____、_____、_____.
(3)通过实验得出的结论是:_____.
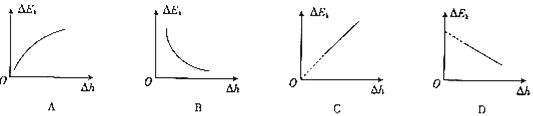
(4)根据该实验,请你判断下列△Ek﹣△h图象中正确的是_____.