题目内容
【题目】如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德(GAtwood 1746﹣1807)创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.
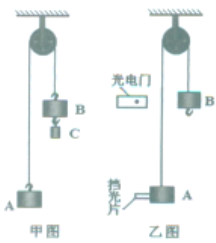
(1)实验时,该同学进行了如下步骤:
①将质量均为M(A的含挡光片、B的含挂钩)的重物用绳连接后,跨放在定滑轮上,处于静止状态.测量出 (填“A的上表面”、“A的下表面”或“挡光片中心”)到光电门中心的竖直距离h.
②在B的下端挂上质量为m的物块C,让系统(重物A、B以及物块C)中的物体由静止开始运动,光电门记录挡光片挡光的时间为△t.
③测出挡光片的宽度d,计算有关物理量,验证机械能守恒定律.
(2)如果系统(重物A、B以及物块C)的机械能守恒,应满足的关系式为 (已知重力加速度为g).
(3)引起该实验系统误差的原因有 (写一条即可).
(4)验证实验结束后,该同学突发奇想:如果系统(重物A、B以及物块C)的机械能守恒,不断增大物块C的质量m,重物B的加速度a也将不断增大,那么a与m之间有怎样的定量关系?a随m增大会趋于一个什么值?请你帮该同学解决,
①写出a与m之间的关系式(还要用到M和g):
②a的值会趋于 .
【答案】(1)挡光片中心 (2)![]() (3)绳子有质量、滑轮与绳子之间有摩擦、重物运动受到空气阻力等 (4)①
(3)绳子有质量、滑轮与绳子之间有摩擦、重物运动受到空气阻力等 (4)①![]() ②重力加速度g
②重力加速度g
【解析】
试题分析:(1)(2)验证机械能守恒定律的原理是系统重力势能的减少量等于系统动能的增加量。即需要测量系统重力势能的变化量,则应该测量出挡光片中心到光电门中心的距离,则系统重力势能的减小量![]() ,系统的末速度为:
,系统的末速度为: ![]() ,系统动能的增加量为:
,系统动能的增加量为:![]() 若系统机械能守恒,则有:
若系统机械能守恒,则有:![]() ,
,
故需要测出挡光片中心到光电门中心的距离,关系式为:![]() 。
。
(3)系统机械能守恒的条件是只有重力做功,引起实验误差的原因可能有:绳子有质量、滑轮与绳子之间有摩擦、重物运动受到空气阻力等.
(4)根据牛顿第二定律得,系统所受的合力为mg,由牛顿第二定律:![]()
则系统加速度为: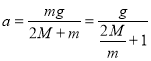 ,当m不断增大,则a趋向于g.
,当m不断增大,则a趋向于g.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案