题目内容
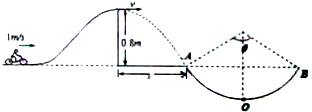
 如图所示,光滑曲面轨道的水平出口跟停在光滑水平面上的平板小车上表面相平,质量为m=2kg的小滑块从光滑轨道上某处由静止开始滑下并滑上小车,使得小车在光滑水平面上滑动.已知小滑块从高为H=0.2m的位置由静止开始滑下,最终停在小车上.若小车的质量为M=6kg.g取10m/s2,求:
如图所示,光滑曲面轨道的水平出口跟停在光滑水平面上的平板小车上表面相平,质量为m=2kg的小滑块从光滑轨道上某处由静止开始滑下并滑上小车,使得小车在光滑水平面上滑动.已知小滑块从高为H=0.2m的位置由静止开始滑下,最终停在小车上.若小车的质量为M=6kg.g取10m/s2,求:(1)滑块到达轨道底端时的速度大小v0
(2)滑块滑上小车后,小车达到的最大速度v
(3)该过程系统产生的内能Q
(4)若滑块和车之间的动摩擦因数为μ=0.1,则车的长度至少为多少?
分析:(1)根据机械能守恒定律求出滑块到达轨道底端时的速度大小.
(2)滑块滑上小车,当两者速度达到相同时,小车的速度最大,根据动量守恒定律求出小车的速度.
(3)根据能量守恒定律求出系统产生的内能.
(4)根据摩擦力与相对路程的乘积等于产生的热量,求出车的最小长度.
(2)滑块滑上小车,当两者速度达到相同时,小车的速度最大,根据动量守恒定律求出小车的速度.
(3)根据能量守恒定律求出系统产生的内能.
(4)根据摩擦力与相对路程的乘积等于产生的热量,求出车的最小长度.
解答:解:(1)滑块从高处运动到轨道底端,机械能守恒.
mgH=
mv02
v0=
=2m/s.
(2)滑块滑上平板车后,系统水平方向上不受外力,动量守恒,小车最大速度与滑块共速的速度.
mv0=(m+M)v
v=
=0.5m/s.
(3)由能的转化与守恒定律知,系统产生的内能等于系统损失的机械能.即:
Q=mgH-
(M+m)v2=
gH=3J,
(4)设小车的长度至少为L.则μmgL=Q
即L=1.5m.
答:(1)滑块到达轨道底端时的速度大小为2m/s.
(2)滑块滑上小车后,小车达到的最大速度为0.5m/s.
(3)该过程系统产生的内能Q为3J.
(4)车的长度至少为1.5m.
mgH=
| 1 |
| 2 |
v0=
| 2gH |
(2)滑块滑上平板车后,系统水平方向上不受外力,动量守恒,小车最大速度与滑块共速的速度.
mv0=(m+M)v
v=
| mv0 |
| M+m |
(3)由能的转化与守恒定律知,系统产生的内能等于系统损失的机械能.即:
Q=mgH-
| 1 |
| 2 |
| Mm |
| M+m |
(4)设小车的长度至少为L.则μmgL=Q
即L=1.5m.
答:(1)滑块到达轨道底端时的速度大小为2m/s.
(2)滑块滑上小车后,小车达到的最大速度为0.5m/s.
(3)该过程系统产生的内能Q为3J.
(4)车的长度至少为1.5m.
点评:本题综合考查了机械能守恒定律、动量守恒定律、能量守恒定律,综合性较强,对学生的能力要求较高,需加强这方面的训练.

练习册系列答案
相关题目
 [物理]
[物理]