题目内容
(12分)如图所示,木板A的质量为m,木板B的质量为2m,置于水平地面上,它们之间距离为L,质量为m的物块C带电量为q,静止于木板A的左端,木板A和木板B与水平地面之间的动摩擦因数都为μ,C与A、B之间的动摩擦因数都为6μ,最大静摩擦力可认为等于滑动摩擦力。开始时,三个物体均处于静止状态。现加一水平向右的匀强电场,电场强度为E=4μmg/q。经过一段时间后物块C最终停留在木板B上某处。假定物块C的电量保持不变且可视为质点,木板A、B碰撞时间极短,碰撞后粘连在一起,电场区域足够大。求:

(1) A与B碰撞后瞬间木板B的速度v1是多大?
(2) C与木板B相对静止时,木板B的速度v2是多大?
(3) 从A与B碰撞到物块C刚相对于木板B静止的过程中,电场力对物块C做的功W是多少?
(1)根据题意可知,A与B碰撞前A和C一起做匀加速运动,设与B碰撞前速度为v0,由动能定理有
![]() ………………………………………………………①
………………………………………………………①
当A与B碰撞时,A、B动量守恒
![]() ……………………………………………………………………②
……………………………………………………………………②
解得![]() ………………………………………………………………③
………………………………………………………………③
(2)A、B相碰后,以A、B、C三者为系统,受到的摩擦力为f,电场力为F,则
f=4μmg
F=qE=4μmg ………………………………………………………………④
F与F大小相等,方向相反,所受合外力为零,所以系统动量守恒,A、B、C速度相等为v2,则
![]() …………………………………………………………⑤
…………………………………………………………⑤
或![]()
解得![]() ……………………………………………………………⑥
……………………………………………………………⑥
(3)设物块C在A与B碰撞后到相对于木板B静止的过程中运动的加速度为a,通过的距离为s,则
![]() ………………………………………………………………⑦
………………………………………………………………⑦
![]() ……………………………………………………………⑧
……………………………………………………………⑧
![]() ……………………………………………………………………⑨
……………………………………………………………………⑨
![]() …………………………………………………………………⑩
…………………………………………………………………⑩
本题满分12分。其中①式2分,②③式各1分;⑤式3分,⑥式1分;⑦⑧⑨⑩式各1分。

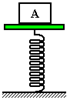 如图所示,木板固定在劲度系数为k的轻质弹簧上,弹簧与地面连在一起.现把质量为m的木块A放在木板上,并用力将木块A向下压,然后突然放手,木块A随即被弹射出去,则在木块A脱离木板之前,木块A的运动情况为( )
如图所示,木板固定在劲度系数为k的轻质弹簧上,弹簧与地面连在一起.现把质量为m的木块A放在木板上,并用力将木块A向下压,然后突然放手,木块A随即被弹射出去,则在木块A脱离木板之前,木块A的运动情况为( ) 如图所示,放在固定的斜面上的木板,其上表面光滑左端有挡板,轻质弹簧左端固定在木板的挡板上,右端与放在木板上的滑块M相连.若滑块和木板相对静止一起沿斜面匀速下滑,不计空气阻力,则木板受力的个数是( )
如图所示,放在固定的斜面上的木板,其上表面光滑左端有挡板,轻质弹簧左端固定在木板的挡板上,右端与放在木板上的滑块M相连.若滑块和木板相对静止一起沿斜面匀速下滑,不计空气阻力,则木板受力的个数是( ) 长为5.25m轻质的薄木板放在水平面上,木板与水平面间的动摩擦因数为0.1,在木板的右端固定有一个质量为1kg的小物体A,在木板上紧邻A处放置另一质量也为1kg的小物体B,小物体B与木板间的动摩擦因数为0.2,A、B可视为质点,如图所示.当A、B之间的距离小于或等于3m时,A、B之间存在大小为6N的相互作用的恒定斥力;当A、B之间的距离大于3m时,A、B之间无相互作用力.现将木板、A、B从图示位置由静止释放,g取10m/s2,求:
长为5.25m轻质的薄木板放在水平面上,木板与水平面间的动摩擦因数为0.1,在木板的右端固定有一个质量为1kg的小物体A,在木板上紧邻A处放置另一质量也为1kg的小物体B,小物体B与木板间的动摩擦因数为0.2,A、B可视为质点,如图所示.当A、B之间的距离小于或等于3m时,A、B之间存在大小为6N的相互作用的恒定斥力;当A、B之间的距离大于3m时,A、B之间无相互作用力.现将木板、A、B从图示位置由静止释放,g取10m/s2,求: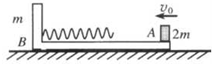
 一斜面固定在水平面上,在斜面顶端有一长木板,木板与斜面之间的动摩擦因数为?,木板上固定一轻质弹簧测力计,弹簧测力计下面固定一个光滑的小球如图所示,木板固定时,弹簧测力计示数为F1,由静止释放后木板沿斜面下滑,稳定时弹簧测力计的示数为F2,斜面的高为h,底边长为d,则下列说法正确的是( )
一斜面固定在水平面上,在斜面顶端有一长木板,木板与斜面之间的动摩擦因数为?,木板上固定一轻质弹簧测力计,弹簧测力计下面固定一个光滑的小球如图所示,木板固定时,弹簧测力计示数为F1,由静止释放后木板沿斜面下滑,稳定时弹簧测力计的示数为F2,斜面的高为h,底边长为d,则下列说法正确的是( )