题目内容
(14分)如图甲，在水平地面上固定一倾角为θ的光滑斜面，一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端，整根弹簧处于自然状态。一质量为m的滑块从距离弹簧上端为s0处由静止释放，设滑块与弹簧接触过程中没有机械能损失，弹簧始终处在弹性限度内，重力加速度大小为g。
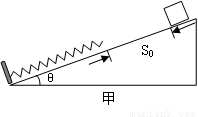
（1）求滑块从静止释放到与弹簧上端接触瞬间所经历的时间t1
（2）若滑块在沿斜面向下运动的整个过程中最大速度大小为vm，求滑块从静止释放到速度大小为vm过程中弹簧的弹力所做的功W
（3）从滑块静止释放瞬间开始计时，请在乙图中画出滑块在沿斜面向下运动的整个过程中速度与时间关系图象。图中横坐标轴上的t1、t2及t3分别表示滑块第一次与弹簧上端接触、第一次速度达到最大值及第一次速度减为零的时刻，纵坐标轴上的v1为滑块在t1时刻的速度大小，vm是题中所指的物理量。（本问不要求写出计算过程）
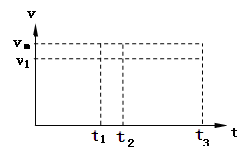
【答案】
（1）
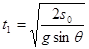
（2）
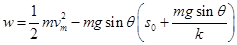（或
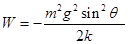）（3）见解析
【解析】
试题分析：（1）滑块从静止释放到与弹簧刚接触的过程中作初速度为零的匀加速直线运动，设加速度大小为a，则有
mgsin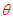
=ma
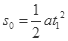2分
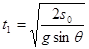2分
2分
（2）滑块速度最大时受力平衡，设此时弹簧压缩量为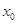
，则有
2分
从静止释放到速度达到最大的过程中，由动能定理得
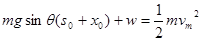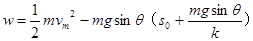2分
2分
或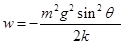 
（3）从开始下滑到和弹簧接触之前，滑块做匀加速运动直线运动，接触弹簧后，滑块先做加速度不断减小的加速运动，直到速度达到最大，随后滑块再做加速度不断增大的减速运动，直到速度减为零，速度随时间的变化图象如下图所示：
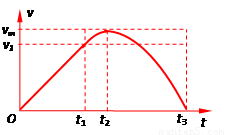
考点：本题考查了牛顿第二定律和动能定理得应用
练习册系列答案
相关题目
，底边BC涂黑，一细束入射光沿平行于底边BC的方向入射，经AB面折射到AC面，则此束光能否从AC面射出？
之间的关系为：
， 
=1.1, 
= 1×105nm2
, 
=1.3,
= 5×104nm2