��Ŀ����
A����ͼ����ʾ������Ϊm�IJ������ԵС���B��ֹ��b�㣬��Եˮƽ���abc���Ե�⻬Բ�����cdƽ�����ӣ�dΪcd�������ߵ㣮����Ϊm������Ϊ+q��С���A�Գ��ٶ�v0=
��a�㿪ʼˮƽ�����˶�������b����С���B������������ײ��A��Bճ����һ���ٷ��룮���ͬʱ���ڷֽ���bb'��ֽ���cc'֮��Ŀռ��ڸ���һˮƽ����ĵ糡����С���AB����糡ʱΪt=0ʱ�̣��糡��ʱ��仯��ͼ����ͼ����ʾ����֪��ǿE=
��T0=
��a��b�������Ϊl0���糡�Ŀ���Ϊ
��L��l0��d��߶�Ϊl0��С���A��B��ˮƽ����Ķ�Ħ��������=0.5������Ħ�����ƣ�С���A��B����Ϊ�ʵ㣮�������ٶ���g��ʾ����
��1��С���A����b�㼴����С���B��ײǰ���ٶ�vA��С��
��2����С���A��a�㿪ʼ�˶���С���A��B��һ���뿪�糡�������������������Ħ������С���A��B�����ܹ�Wf��L�Ĺ�ϵ
��3���ж�С���AB�ܷ��ϻ���cd�����d�㣮

B����ͼ����ʾ��a��b������ԭ��������һ�𣬾�ֹ��ˮƽ���ϵ�A�㣬����a��b�������ֱ�Ϊm��2m�������ˮƽ�����Ķ�Ħ������Ϊ0.1��B��ΪԲ�������͵㣬A��B֮��ľ���Ϊ5R������a��b��ij��������������ͻȻ�ֿ���a��va=3
���ٶ���A�㿪ʼ��B�㻬�У������Ϲ⻬�İ뾶ΪR��
Բ��BC����C�����Ϸ���һ��C��߶�ҲΪR����תƽ̨����ƽֱ̨�����������������ľ�����ȵ�С��P��Q����תʱ�����ܴﵽC������Ϸ��������黬��C����P��������ǡ�ܴ�Q�����£���
��1���ֿ���b���õ��ٶ�vb
��2������a��B��ʱ�Թ����ѹ����
��3������������P��ʱ���ٶ�vP
��4��ƽ̨ת���Ľ��ٶȦ�Ӧ����ʲô������
| 7gl0 |
| 2mg |
| q |
|
| l0 |
| 4 |
��1��С���A����b�㼴����С���B��ײǰ���ٶ�vA��С��
��2����С���A��a�㿪ʼ�˶���С���A��B��һ���뿪�糡�������������������Ħ������С���A��B�����ܹ�Wf��L�Ĺ�ϵ
��3���ж�С���AB�ܷ��ϻ���cd�����d�㣮

B����ͼ����ʾ��a��b������ԭ��������һ�𣬾�ֹ��ˮƽ���ϵ�A�㣬����a��b�������ֱ�Ϊm��2m�������ˮƽ�����Ķ�Ħ������Ϊ0.1��B��ΪԲ�������͵㣬A��B֮��ľ���Ϊ5R������a��b��ij��������������ͻȻ�ֿ���a��va=3
| gR |
| 1 |
| 4 |
��1���ֿ���b���õ��ٶ�vb
��2������a��B��ʱ�Թ����ѹ����
��3������������P��ʱ���ٶ�vP
��4��ƽ̨ת���Ľ��ٶȦ�Ӧ����ʲô������
��������A���ѵ��Ǽ��������������ڵ糡���ٶȼ�Ϊ��ʱ���������λ��S��ʱ��t���ٽ��ڵ糡���˶���ʱ����2
���Ƚϣ��Ӷ��������ۣ�B���ѵ����ڻ��黬��C����P��������ǡ�ܴ�Q������Qת���ĽǶ������=�У���+2��=3�У���+4��=5�С�������д����=��2n+1���б���ʽ��Ȼ���=��t��⣮
| T | 0 |
����⣺A����1��С���A��a�㻬��b�㣬���ܶ���-��mgl0=
m
-
m
��
=
��С���A����b�㼴����С���B��ײǰ���ٶ�vA��СΪ
��2��A��B��ײ���������ٶ�Ϊv�������غ㶨��mvA=2mv
�ã�v=
ABһ���ڵ糡�����˶������ٶ�Ϊ0ʱ��λ��ΪS�����ܶ���-(qE+��.2mg)s=0-
.2m
��E=
����ã�s=
�����Ҽ��ٹ����� qE+��.2mg=2ma1 �ã�a1=
g
����Ϊ0����ʱ��Ϊ��t1=
=
��������ٹ����� qE-��.2mg=2ma2 �ã�a2=
g
��s=
a2
�ɵõ�����߽�bb'��ʱ�䣺t2=
�����ڵ糡����˶�ʱ�䣺tm=t1+t2=
(
+1)=(
+1)T0 ��tm��2T0����С���AB��bb'��cc'֮���˶�ʱ��һֱ�ܵ��糡�����ã�
�������£�
�ٵ�
��L��
ʱ��L��s��AB���Դ����糡�ұ߽�cc'��Wf=-(��mgl0+��.2mgL)=-mg(L+
l0)
�ڵ�
��L��l0ʱ��L��s��AB�ڵ糡�������������˶����ٶȼ�Ϊ0������qE=2mg��f=mg����AB���������٣�����߽�bb'�뿪�糡����Wf=-(��mgl0+��.2mg.2s)=-
mgl0
����
��L��
ʱWf=-(��mgl0+��.2mgL)=-mg(L+
l0)
��
��L��l0ʱ
=-
m
��3���ٵ�
��L��
��AB��Խ�糡���ұ߽�cc'���赽��c�Ķ���ΪEKc
�ɶ��ܶ�����-(��.2mg+qE)L=EKc-
.2m
�ã�Ekc=
mgl0-3mgL
����0��Ekc��
mgl0
���� Ekc��2mgl0�����ܵ���d�㣮
�ڵ�
��L��l0ʱ��AB����߽�bb'�뿪�糡�����ܵ���d�㣮
��
B���⣺
��1��a��b�ֿ��Ĺ��̣�ѡ���ҷ���Ϊ�������ɶ����غ��mva-2mvb=0
��֮�ã�vb=
��2���軬����B��ʱ�ٶ�ΪvB���Ի�����A�㵽B��Ӧ�ö��ܶ����У�-��mg?5R=
m
-
m
�Ի�����B�㣬��ţ�ٵڶ������У�FN-mg=m
��ã�FN=9mg
��ţ�ٵ������ɿ�֪��������B��ʱ�Թ����ѹ����С
=FN=9mg ������ֱ���£�
��3�������B�㿪ʼ�˶����е���غ㣬�軬�鵽��P��ʱ�ٶ�ΪvP����
m
=
m
+mg?2R
��ã�vP=2
��4�����鴩��P���ٻص�ƽ̨��ʱ�䣺t=
=4
Ҫ��ʵ���������̣������㣺��t=��2n+1����
����=
(n=0��1��2��)
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 0 |
��
| v | A |
| 6gl0 |
��С���A����b�㼴����С���B��ײǰ���ٶ�vA��СΪ
6
|
��2��A��B��ײ���������ٶ�Ϊv�������غ㶨��mvA=2mv
�ã�v=
| ||
| 2 |
ABһ���ڵ糡�����˶������ٶ�Ϊ0ʱ��λ��ΪS�����ܶ���-(qE+��.2mg)s=0-
| 1 |
| 2 |
| v | 2 |
��E=
| 2mg |
| q |
| l0 |
| 2 |
�����Ҽ��ٹ����� qE+��.2mg=2ma1 �ã�a1=
| 3 |
| 2 |
����Ϊ0����ʱ��Ϊ��t1=
| v |
| a1 |
|
��������ٹ����� qE-��.2mg=2ma2 �ã�a2=
| 1 |
| 2 |
��s=
| 1 |
| 2 |
| t | 2 2 |
|
�����ڵ糡����˶�ʱ�䣺tm=t1+t2=
|
| ||
| 3 |
| ||
| 3 |
�������£�
�ٵ�
| l0 |
| 4 |
| l0 |
| 2 |
| 1 |
| 2 |
�ڵ�
| l0 |
| 2 |
| 3 |
| 2 |
����
| l0 |
| 4 |
| l0 |
| 2 |
| 1 |
| 2 |
��
| l0 |
| 2 |
| W | f |
| 3 |
| 2 |
| gl | 0 |
��3���ٵ�
| l0 |
| 4 |
| l0 |
| 2 |
�ɶ��ܶ�����-(��.2mg+qE)L=EKc-
| 1 |
| 2 |
| v | 2 |
�ã�Ekc=
| 3 |
| 2 |
����0��Ekc��
| 3 |
| 4 |
���� Ekc��2mgl0�����ܵ���d�㣮
�ڵ�
| l0 |
| 2 |
��
B���⣺
��1��a��b�ֿ��Ĺ��̣�ѡ���ҷ���Ϊ�������ɶ����غ��mva-2mvb=0
��֮�ã�vb=
| 3 |
| 2 |
| gR |
��2���軬����B��ʱ�ٶ�ΪvB���Ի�����A�㵽B��Ӧ�ö��ܶ����У�-��mg?5R=
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 a |
�Ի�����B�㣬��ţ�ٵڶ������У�FN-mg=m
| ||
| R |
��ã�FN=9mg
��ţ�ٵ������ɿ�֪��������B��ʱ�Թ����ѹ����С
| F | �� N |
��3�������B�㿪ʼ�˶����е���غ㣬�軬�鵽��P��ʱ�ٶ�ΪvP����
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 P |
��ã�vP=2
| gR |
��4�����鴩��P���ٻص�ƽ̨��ʱ�䣺t=
| ||
| g |
|
Ҫ��ʵ���������̣������㣺��t=��2n+1����
����=
| (2n+1)�� |
| 4 |
|
���������������Ĺؼ������������̵ķ��������ݲ�ͬ���������̽�������ģ����ʽ��⣮

��ϰ��ϵ�д�
�����Ŀ
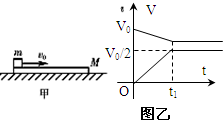 ��ͼ����ʾ������ΪM��ľ�徲ֹ�ڹ⻬ˮƽ���ϣ�һ������Ϊm��С�����Գ��ٶȦ�0��ľ���������һ���ľ�壮�����ľ���ٶ���ʱ��仯��ͼ����ͼ����ʾ��ijͬѧ����ͼ����������һЩ�жϣ���ȷ���ǣ�������?
��ͼ����ʾ������ΪM��ľ�徲ֹ�ڹ⻬ˮƽ���ϣ�һ������Ϊm��С�����Գ��ٶȦ�0��ľ���������һ���ľ�壮�����ľ���ٶ���ʱ��仯��ͼ����ͼ����ʾ��ijͬѧ����ͼ����������һЩ�жϣ���ȷ���ǣ�������?
 ��ͼ����ʾ������Ϊm=0.5kg�����ٶ�v0=10m/s�����壬�ܵ�һ������ٶ�v0�����෴������F���ã��شֲڵ�ˮƽ�滬��������������Ķ�Ħ������Ϊ�̣���3s��ȥ������ֱ������ֹͣ���������������v-tͼ����ͼ����ʾ ��g=10m/s2���� ������
��ͼ����ʾ������Ϊm=0.5kg�����ٶ�v0=10m/s�����壬�ܵ�һ������ٶ�v0�����෴������F���ã��شֲڵ�ˮƽ�滬��������������Ķ�Ħ������Ϊ�̣���3s��ȥ������ֱ������ֹͣ���������������v-tͼ����ͼ����ʾ ��g=10m/s2���� ������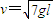 ��a�㿪ʼˮƽ�����˶�������b����С���B������������ײ��A��Bճ����һ���ٷ��룮���ͬʱ���ڷֽ���bb'��ֽ���cc'֮��Ŀռ��ڸ���һˮƽ����ĵ糡����С���AB����糡ʱΪt=0ʱ�̣��糡��ʱ��仯��ͼ����ͼ����ʾ����֪��ǿ
��a�㿪ʼˮƽ�����˶�������b����С���B������������ײ��A��Bճ����һ���ٷ��룮���ͬʱ���ڷֽ���bb'��ֽ���cc'֮��Ŀռ��ڸ���һˮƽ����ĵ糡����С���AB����糡ʱΪt=0ʱ�̣��糡��ʱ��仯��ͼ����ͼ����ʾ����֪��ǿ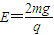 ��
��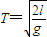 ��a��b�������Ϊl���糡�Ŀ���Ϊ
��a��b�������Ϊl���糡�Ŀ���Ϊ 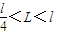 ��d��߶�Ϊl��С���A��B��ˮƽ����Ķ�Ħ��������=0.5������Ħ�����ƣ�С���A��B����Ϊ�ʵ㣮�������ٶ���g��ʾ����
��d��߶�Ϊl��С���A��B��ˮƽ����Ķ�Ħ��������=0.5������Ħ�����ƣ�С���A��B����Ϊ�ʵ㣮�������ٶ���g��ʾ����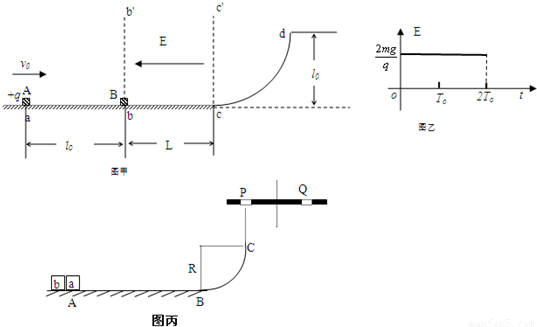
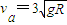 ���ٶ���A�㿪ʼ��B�㻬�У������Ϲ⻬�İ뾶ΪR��
���ٶ���A�㿪ʼ��B�㻬�У������Ϲ⻬�İ뾶ΪR��  Բ��BC����C�����Ϸ���һ��C��߶�ҲΪR����תƽ̨����ƽֱ̨�����������������ľ�����ȵ�С��P��Q����תʱ�����ܴﵽC������Ϸ��������黬��C����P��������ǡ�ܴ�Q�����£���
Բ��BC����C�����Ϸ���һ��C��߶�ҲΪR����תƽ̨����ƽֱ̨�����������������ľ�����ȵ�С��P��Q����תʱ�����ܴﵽC������Ϸ��������黬��C����P��������ǡ�ܴ�Q�����£���