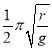Question

【题目】如图甲所示，固定粗粗糙斜面的倾角为37°，与斜面平行的轻弹簧下端固定在C处，上端连接质量为1 kg的小滑块（视为质点），BC为弹簧的原长．现将滑块从A处由静止释放，在滑块从释放至第一次到达最低点的过程中，其加速度a随弹簧的形变量x的变化规律如图乙所示（取沿斜面向下为加速度的正方向），取sin37°= 0.6，cos37°=0.8，g=10m/s2.下列说法正确的是

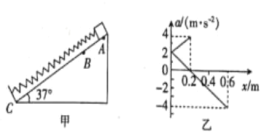
A.滑块到达B处时的速度最大

B.弹簧的劲度系数为10 N/m

C.滑块与斜面间的动摩擦因数为0.5

D.从滑块被释放至第一次运动到最低点的过程中，弹簧的弹性势能的增加量为1.6J

Answer 1

【答案】BCD

【解析】

A．经分析可知，当滑块在B处下方0.2 m处时，滑块的加速度为零、速度最大．故A错误．BC．滑块所受重力沿斜面向下的分力大小G1=mgsin37°=6N，滑块对斜面的压力大小N=mgcos37°=8N，滑块在B点上方时，根据牛顿第二定律有：G1+kx-μN=ma，解得：

a=kx+6-8μ

结合题图乙可得：

k=N/m=10 N/m

6-8μ=2

即：

μ=0.5

故BC正确．

D．滑块刚释放时，弹簧的伸长量x1=0.2 m，滑块在较低点时，弹簧的压缩量x2=0. 6 m，滑块从释放到第一次到达最低点的过程中，因摩擦产生的热量：

Q=μN（x1+x2）=3.2J

根据能量守恒定律可知，从滑块被释放至第一次到达最低点的过程中，弹簧弹性势能的增加量：

△Ep=G1（x1+x2）-Q=1.6J

故D正确．