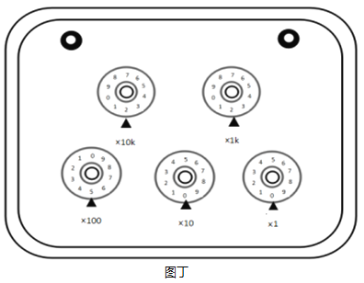
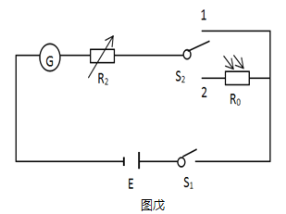
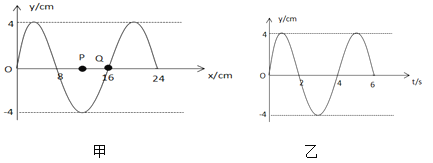
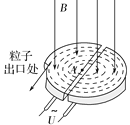
��Ŀ����
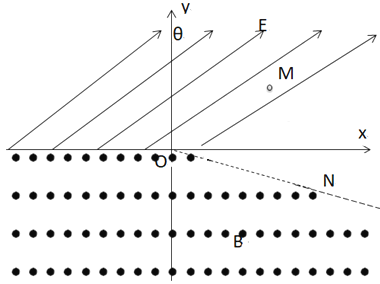
����Ŀ����ͼ����x���Ϸ���ƽ����ֽ�����ǿ�糡���糡ǿ�ȴ�СΪE��������y���������=60������x���·��д�ֱ��ֽ��������н���ǿ�ų����ų����ϱ߽�ON��x���������=15�������±߽�ƽ����x�����ڵ糡��M���ɾ�ֹ�ͷ�һ����Ϊm�������Ϊq�Ĵ��������������糡���ٺ����պô�����ԭ��O����ų�����֪MO=L�������Ӵӱ߽�ON�ϵ�P��(ͼ��δ����)�뿪�ų������ٴν���糡�����糡ƫתǡ�ûص�O�����������ӵ���������
(1)���ӽ���ų�ʱ���ٶȴ�С��
(2)�ų��±߽絽x�����С���룻
(3)�����Ⱥ����ξ���O���ʱ������
���𰸡�(1)![]() (2)
(2)![]() (3)
(3)![]()
��������
(1)���Ӵ�M��O���ȼ���ֱ���˶����ɶ��ܶ����ɵã������뿪�糡����ų�ʱ���ٶȣ�
(2)�������ӵ��˶��켣���������ڵ糡�е���ƽ���˶��ɳ������ڴų����˶��İ뾶���ɼ��ι�ϵ����±߽絽x�����С�����������ڴų����˶��뾶�Ĺ�ϵ��
(3)�����Ⱥ����ξ���O���м����Բ���˶�������ֱ���˶�����ƽ���˶����ֱ���������˶���ʱ�䣬��Ӻ�ɵ������Ⱥ����ξ���O���ʱ������
(1)���Ӵ�M��O���ȼ���ֱ���˶����ɶ��ܶ����ɵã�![]() ����ã����ӽ���ų�ʱ���ٶ�
����ã����ӽ���ų�ʱ���ٶ�![]()
(2)���������ڴų��͵糡�е��˶��켣��ͼ��

���Ӹպúʹų��±߽�����ʱ���ų��±߽絽x��ľ�����С
�ɼ��ι�ϵ�ã�![]()
���Ӵ�Q�����糡������ƽ���˶��ص�O�㣬��![]() ��
��![]()
��ã�![]() ��
��![]() ��
��![]()
��ų��±߽絽x�����С����Ϊ![]()
(3)�����Ⱥ����ξ���O���м����Բ���˶�������ֱ���˶�����ƽ���˶������˶�
�����ڴų��������ķ�֮�����ڣ���![]()
�����뿪�ų����ٴν���糡������������ֱ���˶����ɼ��ι�ϵ�ã�![]()
������ֱ���˶���ʱ��![]()
�����Ⱥ����ξ���O���ʱ����![]()