��Ŀ����
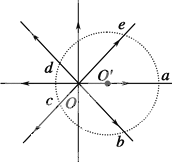
����Ŀ����ͼ���ֲ�ֱ���AB��![]() m����ˮƽ����ļн�
m����ˮƽ����ļн�![]() �����߹��BC�⻬���㹻����������B���⻬���ӣ�һ����
�����߹��BC�⻬���㹻����������B���⻬���ӣ�һ����![]() kg��С����ֹ��A�㣬��ƽ����б�����ϵĺ㶨����F���������˶���B�㣬Ȼ��ȥ����F��С����BC������������߶�
kg��С����ֹ��A�㣬��ƽ����б�����ϵĺ㶨����F���������˶���B�㣬Ȼ��ȥ����F��С����BC������������߶�![]() m��С����б��䶯Ħ������
m��С����б��䶯Ħ������![]() ����gȡ10m/s2��
����gȡ10m/s2�� ![]() ��
�� ![]() ����
����

��1��С����B��ʱ���ٶȴ�С��
��2������F�Ĵ�С��
��3��С���ص�A��ʱ���ܣ�
���𰸡���1��4m/s��2��2.84N��3��2.946J
����������1����BC����⻬��С����BC���˶�ʱֻ��������������е���غ㣬��С����B������ߴ��Ļ�е����ȣ�������ߴ�ʱ�ٶ�Ϊ�㡣���ݻ�е���غ㶨�ɣ�
![]()
�������ݵ� vB=4m/s
��2��С������������ͼ
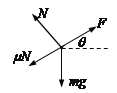
С����AB���ܺ������ã����ȼ����˶�
���vB2=2as
��![]()
��ţ�ٶ���F-mgsin��-��N=ma
N=mgcos��
��F =ma+mgsin��+��mgcos��
�������ݵ�F=2.84N
��3��С������B����ٶ� ������ʱ�ٶ������С������ߵ�ص�B��ʱv��B=vB=4m/s
��B�㷵��A��Ĺ����У�����ͼ��ͼ
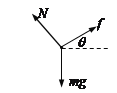
mgsin��-f=ma2
f=��N
N=mgcos��
�����ã�a2=gsin��-��gcos��
�������ݵ�a2=2.8m/s2
��С���ص�A����ٶ�ΪvA
vA2= vB2+2a2s �������ݵ�vA2=24.96m2/s2
![]() �������ݵ�EKA=2.946J
�������ݵ�EKA=2.946J