Question

【题目】如图所示，飞行器P绕某星球做匀速圆周运动，星球相对飞行器的张角为θ，已知万有引力常量G，下列说法正确的是（　　）

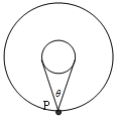
A. 若测得周期和张角，可得到星球的质量

B. 若测得周期和轨道半径，可得到星球的平均密度

C. 若测得周期、轨道半径和张角，可得到星球表面的重力加速度

D. 若测得周期、轨道半径和张角，可得到飞行器的向心力

Answer 1

【答案】C

【解析】

飞行器绕某星球做匀速圆周运动，由星球的万有引力提供向心力，根据万有引力定律和几何知识、密度公式可求解星球的平均密度；星球表面物体的重力等于万有引力，可以求出星球表面的重力加速度，据此分析需要测量的物理量。

A、B项：设星球的质量为M，半径为R，平均密度为ρ．张角为θ，飞行器的质量为m，轨道半径为r，周期为T．对于飞行器，根据万有引力提供向心力得：

由几何关系有：

星球的质量：

由以上三式得，可知测出周期和轨道半径可以求出星球的质量；

星球密度，知测得周期和张角可得到星球的平均密度，故AB错误；

C项：由AB分析知，由周期和轨道半径可以求出星球的质量，由轨道半径和张角可求出星球半径，根据星球表面物体的重力等于万有引力，有，得，所以知测得周期、轨道半径和张角，可得到星球表面的重力加速度。故C正确；

D项：因为不知道飞行器的质量，所以无法得到飞行器的向心力，故D错误。

故应选：C。