��Ŀ����
����Ŀ����ͼ��ʾΪ�뾶ΪR�İ�Բ���β���ש�ĺ���棬OΪ�ú�����Բ�ġ����� PQ������AB��30���ǵķ������벣��ש�������Q��Բ��O�ľ���Ϊ![]() ������ǡ�ôӲ���ש���е�E�������֪��������еĴ����ٶ�Ϊc��
������ǡ�ôӲ���ש���е�E�������֪��������еĴ����ٶ�Ϊc��
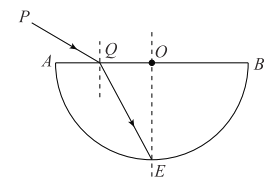
(1)����ש�������ʼ����ߴ�Q�㴫����E�����õ�ʱ�䣻
(2)��ʹ����PQ����ƽ�ƣ����ƶ�������ʱǡ����ʹ���ߴ�Բ��������������Ǿ���Բ���ڱ��淴�������Ĺ⣩��
���𰸡�(1)![]() (2)
(2)![]()
��������
(1)����PQ���䵽����ש���棬�����![]() �����Ӧ�������QE�������Ϊ
�����Ӧ�������QE�������Ϊ![]() ����ͼ��ʾ��
����ͼ��ʾ��
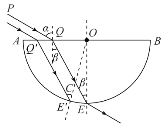
�ɼ��ι�ϵ�ã�
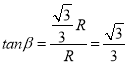 ��
��
����
![]()
�������䶨���У�
![]()
��ã�
![]()
����QE�ڲ���ש�ڴ������ٶ�Ϊ��
![]()
�����ľ���Ϊ��
![]()
���ߴ�Q�㴫����E�����õ�ʱ�䣺
![]() ��
��
(2)��ʹ����PQ����ƽ�ƾ���x���������![]() �� ����Բ����������ǡ�õ����ٽ��C����
�� ����Բ����������ǡ�õ����ٽ��C����
![]()
��![]() Ӧ�����Ҷ����У�
Ӧ�����Ҷ����У�
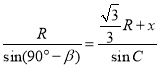
������ã�
![]() ��
��

��ϰ��ϵ�д�
�����Ŀ




