题目内容
13. 如图所示,质量为m的A球和质量为2m的B球用挡板挡住,静止在光滑斜面上,斜面倾角为θ,A球左边的挡板竖直,B球左边挡板垂直斜面.
如图所示,质量为m的A球和质量为2m的B球用挡板挡住,静止在光滑斜面上,斜面倾角为θ,A球左边的挡板竖直,B球左边挡板垂直斜面.求:(1)斜面对A球和B球的支持力之比?
(2)挡板对A球和对B球的支持力之比.
分析 两种情况下球均受重力、挡板和斜面对球体的弹力,三力平衡,两个弹力的合力与重力等值、反向、共线,先分别求出两种情况下的支持力,然后求出比值即可.
解答 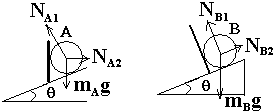 解:对A:$\begin{array}{l}{N_{A1}}cosθ={m_A}g\\{N_{A1}}sinθ={N_{A2}}\end{array}$
解:对A:$\begin{array}{l}{N_{A1}}cosθ={m_A}g\\{N_{A1}}sinθ={N_{A2}}\end{array}$
对B:$\begin{array}{l}{m_B}gcosθ={N_{B1}}\\{m_B}gsinθ={N_{B2}}\end{array}$
解得:$\frac{{{N_{A1}}}}{{{N_{B1}}}}=\frac{1}{{2{{cos}^2}θ}}$;$\frac{{{N_{A2}}}}{{{N_{B2}}}}=\frac{1}{2cosθ}$
答:(1)斜面对A球和B球的支持力之比是$\frac{1}{2{cos}^{2}θ}$;
(2)挡板对A球和对B球的支持力之比是$\frac{1}{2cosθ}$.
点评 本题关键是正确地对球受力分析,然后根据共点力平衡条件并结合合成法求解.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
4. 如图空间固定一正的点电荷+Q,在距电荷距离为d的位置固定一竖直的金属板AB.该板的左侧涂上一层薄的光滑绝缘层.AB的长度是2d,O为AB 的中点且与+Q等高.现将另一质量为m的点电荷+q从A点靠近板的位置释放沿板下滑到B点.+q在此过程中( )
如图空间固定一正的点电荷+Q,在距电荷距离为d的位置固定一竖直的金属板AB.该板的左侧涂上一层薄的光滑绝缘层.AB的长度是2d,O为AB 的中点且与+Q等高.现将另一质量为m的点电荷+q从A点靠近板的位置释放沿板下滑到B点.+q在此过程中( )
 如图空间固定一正的点电荷+Q,在距电荷距离为d的位置固定一竖直的金属板AB.该板的左侧涂上一层薄的光滑绝缘层.AB的长度是2d,O为AB 的中点且与+Q等高.现将另一质量为m的点电荷+q从A点靠近板的位置释放沿板下滑到B点.+q在此过程中( )
如图空间固定一正的点电荷+Q,在距电荷距离为d的位置固定一竖直的金属板AB.该板的左侧涂上一层薄的光滑绝缘层.AB的长度是2d,O为AB 的中点且与+Q等高.现将另一质量为m的点电荷+q从A点靠近板的位置释放沿板下滑到B点.+q在此过程中( )| A. | 加速度先增大后减小 | B. | 在O点速度为$\sqrt{2gd}$ | ||
| C. | 在O点机械能最小 | D. | O点到B点机械能守恒 |
8.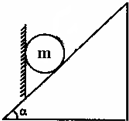 如图所示,光滑球的质量为m,放在竖直挡板和倾角为α的固定斜面间.若缓慢转动挡板至与斜面垂直,此过程中( )
如图所示,光滑球的质量为m,放在竖直挡板和倾角为α的固定斜面间.若缓慢转动挡板至与斜面垂直,此过程中( )
 如图所示,光滑球的质量为m,放在竖直挡板和倾角为α的固定斜面间.若缓慢转动挡板至与斜面垂直,此过程中( )
如图所示,光滑球的质量为m,放在竖直挡板和倾角为α的固定斜面间.若缓慢转动挡板至与斜面垂直,此过程中( )| A. | m对挡板的压力先减小后增大 | B. | m对挡板的压力逐渐减小 | ||
| C. | m对斜面的压力先减小后增大 | D. | m对斜面的压力逐渐增大 |
18.电吹风机中有电动机和电热丝两部分,已知电动机线圈的电阻为R1,它和阻值为R2的电热丝串联.设电吹风机工作时两端的电压为U,通过线圈的电流为I,消耗的电功率为P,则下列关系正确的是( )
| A. | P>UI | B. | P=I2(R1+R2) | C. | P>I2(R1+R2) | D. | U=I(R1+R2) |
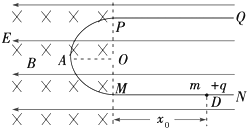 在如图所示的竖直平面内有范围足够大、水平向左的匀强电场,在虚线的左侧有垂直纸面向里的匀强磁场,磁感应强度大小为B,一绝缘?形杆由两段直杆和一半径径为R的半圆环组成,固定在纸面所在的竖直平面内,PQ、MN水平且足够长,半圆环MAP在磁场边界左侧,P、M点在磁场边界线上,NMAP段光滑,PQ段粗糙,现在有一质量为m、带电荷量为+q的小环套在MN杆上,它所受电场力为重力的$\frac{1}{2}$倍.现在M点右侧的D点由静止释放小环,小环刚好能到达P点.
在如图所示的竖直平面内有范围足够大、水平向左的匀强电场,在虚线的左侧有垂直纸面向里的匀强磁场,磁感应强度大小为B,一绝缘?形杆由两段直杆和一半径径为R的半圆环组成,固定在纸面所在的竖直平面内,PQ、MN水平且足够长,半圆环MAP在磁场边界左侧,P、M点在磁场边界线上,NMAP段光滑,PQ段粗糙,现在有一质量为m、带电荷量为+q的小环套在MN杆上,它所受电场力为重力的$\frac{1}{2}$倍.现在M点右侧的D点由静止释放小环,小环刚好能到达P点. 在地面上方某处的真空室里存在着水平方向的匀强电场,以水平向右和竖直向上为x轴、y轴正方向建立如图所示的平面直角坐标系.一质量为m、带电荷量为+q的微粒从点P($\frac{\sqrt{3}}{3}$l,0)由静止释放后沿直线PQ运动.当微粒到达点Q(0,-l)的瞬间,撤去电场,同时加上一个垂直于纸面向外的匀强磁场(图中未画出),磁感应强度的大小B=$\frac{m}{q}$$\sqrt{\frac{3g}{2l}}$,该磁场有理想的下边界,其他方向范围无限大.已知重力加速度为g.求:
在地面上方某处的真空室里存在着水平方向的匀强电场,以水平向右和竖直向上为x轴、y轴正方向建立如图所示的平面直角坐标系.一质量为m、带电荷量为+q的微粒从点P($\frac{\sqrt{3}}{3}$l,0)由静止释放后沿直线PQ运动.当微粒到达点Q(0,-l)的瞬间,撤去电场,同时加上一个垂直于纸面向外的匀强磁场(图中未画出),磁感应强度的大小B=$\frac{m}{q}$$\sqrt{\frac{3g}{2l}}$,该磁场有理想的下边界,其他方向范围无限大.已知重力加速度为g.求: 如图,光滑斜面的倾角α=30°,在斜面上放置一矩形线框abcd,ab边的边长l1=l m,bc边的边长l2=0.6m,线框的质量m=1kg,电阻R=0.1Ω,线框通过细线与重物相连,重物质量M=2kg,斜面上ef线(ef∥gh)的右方有垂直斜面向上的匀强磁场,磁感应强度B=0.5T,如果线框从静止开始运动,进入磁场最初一段时间是匀速的,ef线和gh的距离s=11.4m,(取g=10m/s2),求:
如图,光滑斜面的倾角α=30°,在斜面上放置一矩形线框abcd,ab边的边长l1=l m,bc边的边长l2=0.6m,线框的质量m=1kg,电阻R=0.1Ω,线框通过细线与重物相连,重物质量M=2kg,斜面上ef线(ef∥gh)的右方有垂直斜面向上的匀强磁场,磁感应强度B=0.5T,如果线框从静止开始运动,进入磁场最初一段时间是匀速的,ef线和gh的距离s=11.4m,(取g=10m/s2),求: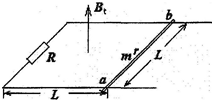 如图所示,质量m=1kg、电阻r=0.5Ω的金属杆a、b置于水平固定的金属轨道上,杆与轨道的摩擦因数μ=0.5,在轨道的一端还接有一只固定电阻,阻值R=2Ω,轨道电阻不计.已知轨道间距和杆离轨道左端的距离均为L=0.5m,垂直穿过轨道平面的匀强磁场从某时刻开始按B1=2-2t(T)的规律变化,取向上为正,g=10m/s2.求:
如图所示,质量m=1kg、电阻r=0.5Ω的金属杆a、b置于水平固定的金属轨道上,杆与轨道的摩擦因数μ=0.5,在轨道的一端还接有一只固定电阻,阻值R=2Ω,轨道电阻不计.已知轨道间距和杆离轨道左端的距离均为L=0.5m,垂直穿过轨道平面的匀强磁场从某时刻开始按B1=2-2t(T)的规律变化,取向上为正,g=10m/s2.求: