题目内容
2. 如图,光滑斜面的倾角α=30°,在斜面上放置一矩形线框abcd,ab边的边长l1=l m,bc边的边长l2=0.6m,线框的质量m=1kg,电阻R=0.1Ω,线框通过细线与重物相连,重物质量M=2kg,斜面上ef线(ef∥gh)的右方有垂直斜面向上的匀强磁场,磁感应强度B=0.5T,如果线框从静止开始运动,进入磁场最初一段时间是匀速的,ef线和gh的距离s=11.4m,(取g=10m/s2),求:
如图,光滑斜面的倾角α=30°,在斜面上放置一矩形线框abcd,ab边的边长l1=l m,bc边的边长l2=0.6m,线框的质量m=1kg,电阻R=0.1Ω,线框通过细线与重物相连,重物质量M=2kg,斜面上ef线(ef∥gh)的右方有垂直斜面向上的匀强磁场,磁感应强度B=0.5T,如果线框从静止开始运动,进入磁场最初一段时间是匀速的,ef线和gh的距离s=11.4m,(取g=10m/s2),求:(1)线框进入磁场前重物M的加速度;
(2)线框进入磁场时匀速运动的速度v;
(3)ab边由静止开始到运动到gh线处所用的时间t;
(4)ab边运动到gh线处的速度大小和在线框由静止开始到运动到gh线的整个过程中产生的焦耳热.
分析 (1)线框进入磁场前,对线框和重物整体,根据牛顿第二定律求解加速度.
(2)线框进入磁场的过程做匀速运动,根据法拉第电磁感应定律、欧姆定律推导出安培力表达式,再根据平衡条件列式,即可求出匀速运动的速度v;
(3)线框abcd进入磁场前时,做匀加速直线运动;进磁场的过程中,做匀速直线运动;进入磁场后到运动到gh线,仍做匀加速直线运动.根据运动学公式可确定运动的时间;
(4)由运动学公式求出ab边运动到gh线处的速度.M的重力势能减小转化为m的重力势能和线框中的内能,根据能量守恒定律求解焦耳热.
解答 解:(1)线框进入磁场前,线框仅受到细线的拉力FT,斜面的支持力和线框重力,重物M受到重力和拉力FT.
对线框,由牛顿第二定律得 FT-mg sinα=ma
联立解得,线框进入磁场前重物M的加速度 a=$\frac{Mg-mgsinα}{M+m}$=$\frac{20-10×\frac{1}{2}}{2+1}$=5m/s2
(2)因为线框进入磁场的最初一段时间做匀速运动,所以重物受力平衡 Mg=FT′,
线框abcd受力平衡 FT′=mg sinα+FA
ab边进入磁场切割磁感线,产生的电动势 E=Bl1v
形成的感应电流 I=$\frac{E}{R}$=$\frac{B{l}_{1}v}{R}$
受到的安培力 FA=BIL1
联立上述各式得,Mg=mg sinα+$\frac{{B}^{2}{l}_{1}^{2}v}{R}$
代入数据解得 v=6m/s
(3)线框abcd进入磁场前时,做匀加速直线运动;进磁场的过程中,做匀速直线运动;进入磁场后到运动到gh线,仍做匀加速直线运动.
进磁场前线框的加速度大小与重物的加速度相同,为a=5 m/s2
该阶段运动时间为 t1=$\frac{v}{a}$=$\frac{6}{5}s$=1.2s
进磁场过程中匀速运动时间 t2=$\frac{{l}_{2}}{v}$=$\frac{0.6}{6}s$=0.1s
线框完全进入磁场后线框受力情况同进入磁场前,所以该阶段的加速度仍为a=5m/s2
s-l2=vt3+$\frac{1}{2}$at${\;}_{3}^{2}$
解得:t3=1.2 s
因此ab边由静止开始运动到gh线所用的时间为 t=t1+t2+t3=2.5s
(4)线框ab边运动到gh处的速度 v′=v+at3=6 m/s+5×1.2 m/s=12m/s
整个运动过程产生的焦耳热 Q=FAl2=(Mg-mgsinθ)l2=9J
答:
(1)线框进入磁场前重物M的加速度是5m/s2;
(2)线框进入磁场时匀速运动的速度v是6m/s;
(3)ab边由静止开始到运动到gh线处所用的时间是2.5s;
(4)ab边运动到gh线处的速度大小和在线框由静止开始到运动到gh线的整个过程中产生的焦耳热是9J
点评 本题是电磁感应与力平衡的综合,安培力的计算是关键.本题中要注意体会运用整体法求解加速度的方法;明确热量焦耳热可以由安培力做功求出.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 甲、乙两个物体组成一系统,甲、乙所受合外力不均为零,则系统的动量不可能守恒 | |
| B. | 用不可见光照射金属一定比用可见光照射同种金属产生的光电子的初动能要大 | |
| C. | 波粒二象性中的波动性是大量光子和高速运动的微观粒子的行为,这种波动性与机械波在本质上是不同的 | |
| D. | 欲使处于基态的氢原子电离,可以用动能为13.7eV的电子去碰撞 | |
| E. | 原子核式结构模型是由汤姆逊在α粒子散射实验基础上提出的 | |
| F. | 发现中子的核反应是${\;}_{4}^{9}$Be+${\;}_{2}^{4}$He→${\;}_{6}^{12}$C+${\;}_{0}^{1}$n | |
| G. | 核力是强相互作用的一种表现,任意两个核子之间都存在核力作用 | |
| H. | β衰变说明了β粒子(电子)是原子核的组成部分 |

| A. | 该波的波长为6m | |
| B. | 该波的周期为12s | |
| C. | 该波的波速为1m/s | |
| D. | 10s末A点的振动速度大于B点的振动速度 |
(1)星球表面的“重力加速度”g;
(2)星球的质量M.
| 规格 | 后轮驱动直流永磁铁电机 | ||
| 车型 | 14电动自行车 | 额定输出功率 | 200W |
| 整车质量 | 40kg | 额定电压 | 48V |
| 最大载重 | 120kg | 额定电流 | 4.5A |
 如图所示,质量为m的A球和质量为2m的B球用挡板挡住,静止在光滑斜面上,斜面倾角为θ,A球左边的挡板竖直,B球左边挡板垂直斜面.
如图所示,质量为m的A球和质量为2m的B球用挡板挡住,静止在光滑斜面上,斜面倾角为θ,A球左边的挡板竖直,B球左边挡板垂直斜面.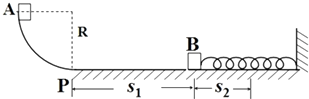 如图所示,轻弹簧的一端固定,另一端与滑块B相连,B静止在水平导轨上,弹簧处在原长状态.滑块A从半径为R的光滑$\frac{1}{4}$圆弧槽无初速滑下,从P点滑上水平导轨,当A滑过距离s1=R时,与B相碰,碰撞时间极短,碰后A、B紧贴在一起运动,但互不粘连.最后A恰好返回出发点P并停止.在A、B压缩弹簧过程始终未超过弹簧的弹性限度.已知滑块A和B质量相同(A、B可视为质点),且与导轨的滑动摩擦因数都为μ=0.1,重力加速度为g.试求:
如图所示,轻弹簧的一端固定,另一端与滑块B相连,B静止在水平导轨上,弹簧处在原长状态.滑块A从半径为R的光滑$\frac{1}{4}$圆弧槽无初速滑下,从P点滑上水平导轨,当A滑过距离s1=R时,与B相碰,碰撞时间极短,碰后A、B紧贴在一起运动,但互不粘连.最后A恰好返回出发点P并停止.在A、B压缩弹簧过程始终未超过弹簧的弹性限度.已知滑块A和B质量相同(A、B可视为质点),且与导轨的滑动摩擦因数都为μ=0.1,重力加速度为g.试求: 有一个标有“2.5V 0.3A”字样的小灯泡,现要测定其在0到2.5V的区间内不同电压下的电功率,并作出其电功率P与其两端电压的平方U2的关系曲线.有下列器材可供选择:
有一个标有“2.5V 0.3A”字样的小灯泡,现要测定其在0到2.5V的区间内不同电压下的电功率,并作出其电功率P与其两端电压的平方U2的关系曲线.有下列器材可供选择: